Taxa de variação média

A taxa de variação média de uma função f entre dois pontos x₁ e x₂ (x₁ ≠ x₂) mede quanto o y muda por unidade de x nesse intervalo. Ela é a inclinação da reta secante que liga (x₁, f(x₁)) a (x₂, f(x₂)). Relembre também: Plano Cartesiano, Gráfico de uma Função e Funções crescente, decrescente e constante.

Fórmula =

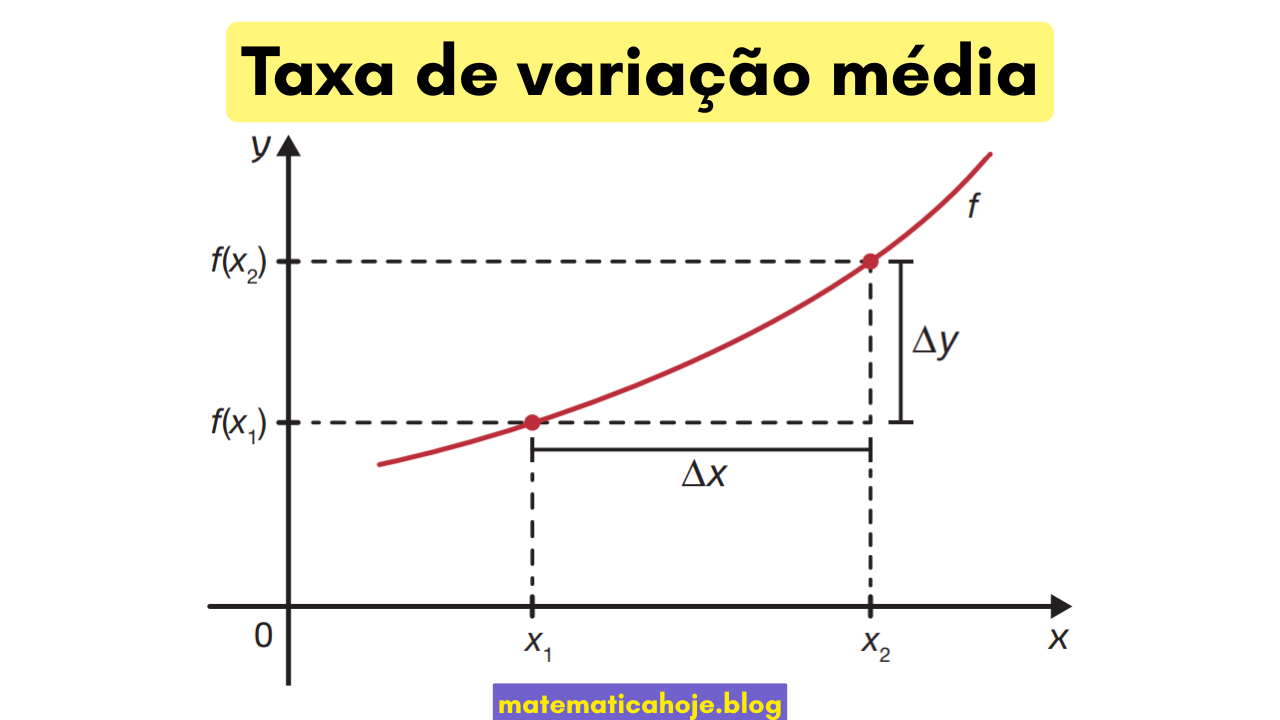
Leitura rápida e significado

Sinal: positiva ⇒ f aumenta no intervalo; negativa ⇒ f diminui; zero ⇒ f ficou constante “em média”.
Unidades: “unidade de y por unidade de x”. Exemplos: km/h, R$/item, °C/h.
Reta y = m x + b: a taxa média em qualquer intervalo é sempre m.
Relação com derivada: quando encurtamos o intervalo (x₂ → x₁), a taxa média tende à taxa instantânea (derivada), se existir.

Exemplos resolvidos

1) Função afim

f(x) = 4x − 7. Entre x = 2 e x = 5:

Taxa média = (f(5) − f(2)) / (5 − 2) = ((20 − 7) − (8 − 7)) / 3 = (13 − 1) / 3 = 12/3 = 4.

2) Quadrática

g(x) = x² − 5x + 6. Entre x = 1 e x = 4:

g(1)=2, g(4)=2 ⇒ (2 − 2)/(4 − 1) = 0 ⇒ 0 (houve descida e subida que se “anulam” no intervalo).

3) Contexto prático (velocidade média)

Um carro parte do repouso e após 3 h percorreu 210 km. Velocidade média = 210 / 3 = 70 km/h (mesmo que a velocidade não tenha sido constante).

4) Sinal negativo

h(x) = −x² em [−1, 2]: h(2)=−4, h(−1)=−1 ⇒ (−4 − (−1))/(2 − (−1)) = (−3)/3 = −1.

Quadro-resumo

Quadro-resumo — Taxa de variação média
Ideia	Como calcular	Como interpretar
Inclinação da secante	(f(x₂) − f(x₁)) / (x₂ − x₁)	Variação “por unidade de x” no intervalo
Sinal	Resultado > 0, < 0 ou = 0	Aumenta, diminui ou fica constante em média
Unidades	Depende de y e de x	km/h, R$/unidade, °C/h, etc.
Reta y = mx + b	Taxa média = m	Independe do intervalo
Ligação com derivada	Limite de Δy/Δx quando Δx → 0	Taxa instantânea (se existir)

📘 Precisa de fórmulas à mão (Bhaskara, médias, porcentagens, derivada básica)? Veja o eBook Fórmulas Matemática.

Armadilhas comuns

Confundir média com instantânea: média usa um intervalo; instantânea é o limite quando o intervalo vai a zero.
Unidades: nunca esqueça de informar (ex.: “reais por item”).
Ordem dos pontos: use (x₂ − x₁) e (f(x₂) − f(x₁)) consistentes — inverter muda o sinal.
Intervalos com subida e descida: a taxa média pode dar zero mesmo com grande “movimento”.

➡️ Praticar taxa de variação no Banco de Questões

Exercícios (múltipla escolha) com solução

1) Para f(x)=2x²−3x+1, a taxa média no intervalo [1,3] é:

Ver solução

f(3)=2·9−9+1=10; f(1)=2−3+1=0 ⇒ (10−0)/(3−1)=10/2=5.

2) A receita R(q)=150q−q² (em R$) de q=10 a q=20 tem taxa média (R$/unidade):

Ver solução

R(20)=3000−400=2600; R(10)=1500−100=1400 ⇒ (2600−1400)/(20−10)=1200/10=120.

3) Uma fábrica passa de 200 para 260 peças em 4 horas. A taxa média de produção (peças/h) é:

Ver solução

Δy=60, Δx=4 ⇒ 60/4=15.

4) Para y=|x|, a taxa média entre x=−2 e x=3 é:

Ver solução

y(3)=3; y(−2)=2 ⇒ (3−2)/(3−(−2))=1/5=0,2.

5) Se a distância (km) é d(t)=40t+10 (t em horas), a taxa média de 1 h a 4 h é:

10 km/h
40 km/h
50 km/h
160 km/h

Ver solução

(d(4)−d(1))/(4−1)=(170−50)/3=120/3=40 km/h.

6) Sobre taxa média e derivada, marque a opção correta:

São sempre iguais.
A taxa média depende de dois pontos; a derivada é o limite quando um ponto se aproxima do outro.
Taxa média só existe para retas.
Derivada não tem unidades físicas.

Ver solução

Correta: (b). A derivada é o limite da taxa média quando Δx → 0 (se existir).