Teorema da Probabilidade Total: Conceito e Exemplos Práticos

O teorema da probabilidade total é uma ferramenta fundamental na probabilidade, usada para calcular a probabilidade de um evento A quando ele pode ocorrer de diferentes formas, associadas a outros eventos B₁, B₂, …, B_n. Esses eventos, chamados de partições do espaço amostral S, ajudam a dividir o problema em partes menores, facilitando os cálculos.

Definição do Teorema da Probabilidade Total

Seja S o espaço amostral e B₁, B₂, …, B_n uma partição de S. Isso significa que:

1. Os eventos B₁, B₂, …, B_n são mutuamente exclusivos (B_i ∩ B_j = ∅ para i ≠ j).
2. A união dos eventos cobre todo o espaço amostral (B₁ ∪ B₂ ∪ … ∪ B_n =S).
3. P(B_k) > 0 para todo k.

Para um evento A, a probabilidade de A pode ser calculada como:

P(A) = P(B₁∩A) + P(B₂∩A) + … + P(B_n∩A)

Usando o teorema da multiplicação, podemos reescrever como:

P(A) = P(B₁)⋅P(A∣B₁) + P(B₂)⋅P(A∣B₂) + … + P(B_n)⋅P(A∣B_n)

Exemplo 1: Escolha de Urnas e Bolas

Problema:
Considere três urnas:

• Urna 1 (B₁): Contém 2 bolas vermelhas e 3 bolas brancas.
• Urna 2 (B₂): Contém 3 bolas vermelhas e 1 bola branca.
• Urna 3 (B₃): Contém 4 bolas vermelhas e 2 bolas brancas.

Uma urna é escolhida ao acaso, e uma bola é retirada. Qual é a probabilidade de a bola retirada ser vermelha (A)?

Solução:

Espaço amostral:
O espaço amostral S considera todas as urnas e as bolas retiradas.

Definir os eventos:

• B₁, B₂, B₃: Eventos de escolha das urnas 1, 2 e 3, respectivamente.
• A: Evento de retirar uma bola vermelha.

Probabilidades:

• P(B₁) = P(B₂) = P(B₃) = 1/3 (urnas escolhidas ao acaso).
• P(A|B₁) = 2/5 (2 bolas vermelhas em 5 na urna 1).
• P(A|B₂)=3/4 (3 bolas vermelhas em 4 na urna 2).
• P(A|B₃) = 4/6 = 2/3 (4 bolas vermelhas em 6 na urna 3).

Aplicando o teorema da probabilidade total:

P(A) = P(B₁)⋅P(A|B₁) + P(B₂)⋅P(A|B₂) + P(B₃)⋅P(A|B₃)

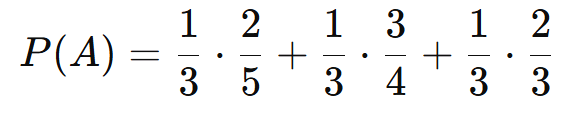
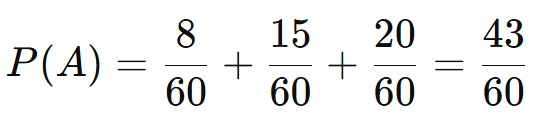
Interpretação:
A probabilidade de a bola retirada ser vermelha é 43/60, ou aproximadamente 71,67%.

Exemplo 2: Problema da Moeda de Bertrand

Problema:
Existem três caixas:

• Caixa 1 (B₁): Contém duas moedas de ouro.
• Caixa 2 (B₂): Contém uma moeda de ouro e uma de prata.
• Caixa 3 (B₃): Contém duas moedas de prata.

Uma caixa é escolhida ao acaso, e uma moeda é retirada. Qual é a probabilidade de a moeda retirada ser de ouro (A)?

Solução:

Espaço amostral:
O espaço amostral S considera todas as caixas e as moedas.

Definir os eventos:

• B₁, B₂, B₃: Eventos de escolha das caixas 1, 2 e 3, respectivamente.
• A: Evento de retirar uma moeda de ouro.

Probabilidades:

• P(B₁) = P(B₂) = P(B₃) = 1/3 (caixas escolhidas ao acaso).
• P(A|B₁) = 1 (todas as moedas da caixa 1 são de ouro).
• P(A|B₂) = 1/2 (metade das moedas da caixa 2 são de ouro).
• P(A|B₃) = 0 (nenhuma moeda da caixa 3 é de ouro).

Aplicando o teorema da probabilidade total:

P(A) = P(B₁)⋅P(A|B₁) + P(B₂)⋅P(A|B₂) + P(B3)⋅P(A|B₃)

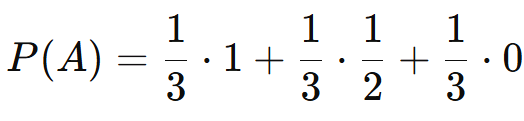
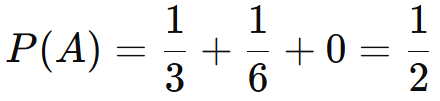
Interpretação:
A probabilidade de a moeda retirada ser de ouro é 1/2, ou 50%.

Conclusão

O teorema da probabilidade total simplifica o cálculo de probabilidades ao dividir o espaço amostral em partes menores e mais fáceis de lidar. Ele é amplamente aplicado em problemas de probabilidade que envolvem partições do espaço amostral, como urnas, caixas ou outros cenários semelhantes. Com a prática e o entendimento desse teorema, é possível resolver problemas complexos de forma clara e estruturada.