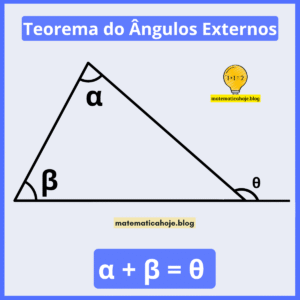
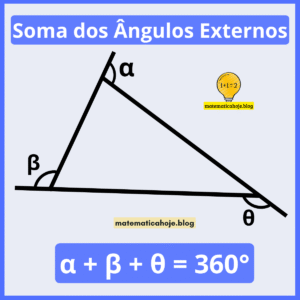
Triângulo Acutângulo — propriedades, fórmulas (uma por linha), exemplos e exercícios
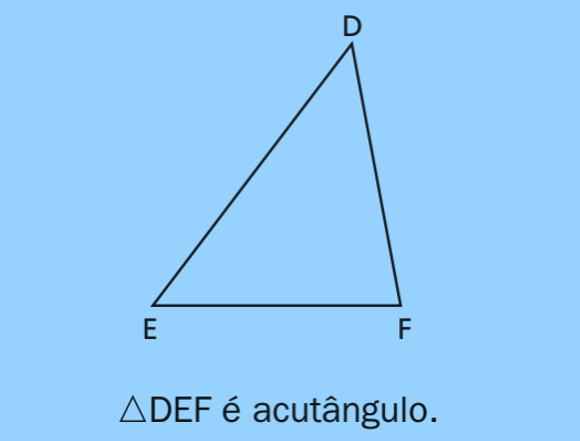
O que é um triângulo acutângulo?
Um triângulo é acutângulo quando todos os seus ângulos internos são agudos, isto é, cada um mede menos que \(90^\circ\). Qualquer triângulo pode ser classificado por ângulos em: acutângulo, retângulo ou obtusângulo. Para revisar todos os tipos por lados e ângulos, visite Tipos de Triângulos.
Na imagem, nenhum ângulo forma canto reto, logo é acutângulo. Em provas, reconhecer isso rapidamente evita cálculos desnecessários.
Como reconhecer rapidamente um triângulo acutângulo
1) Pela medida dos ângulos
- Se \( \max(\angle A,\angle B,\angle C) < 90^\circ \Rightarrow \) acutângulo.
2) Pelos lados (Pitágoras ao contrário)
Sejam \(a,b,c\) os lados e \(c\) o maior. Então:
Essa versão vem da lei dos cossenos e é muito útil quando só temos comprimentos.
Propriedades que valem em qualquer acutângulo
- Alturas se intersectam dentro do triângulo (ortocentro interno).
- Medianas e bissetrizes também intersectam internamente (baricentro e incentro internos).
- Circuncentro (interseção das mediatrizes) fica dentro do triângulo — diferente do obtusângulo, onde pode ser externo.
- Para qualquer lado \(a\) e ângulo oposto \(A\): \( \displaystyle A_\triangle=\frac{bc\sin A}{2} \) e \( \displaystyle h_a=\frac{2A_\triangle}{a} \).
Para estudar os pontos notáveis (baricentro, incentro, circuncentro e ortocentro) em detalhe, consulte Pontos Notáveis do Triângulo. Resumos prontos nos Mapas Mentais.
Fórmulas úteis (uma por linha, com cores)
Precisa relembrar formas de calcular a área? Esse artigo reúne todas, inclusive as que mais caem no ENEM. A coleção 10 eBooks traz quadros-resumo de acutângulo, retângulo e obtusângulo.
Exemplos resolvidos (passo a passo vertical)
Exemplo 1 — Mostre que o triângulo de lados \(a=7\), \(b=8\), \(c=9\) é acutângulo.
Mostrar solução
O maior lado é \(c=9\). Teste de Pitágoras ao contrário:
\(c^2 \stackrel{?}{<} a^2+b^2\)
\(9^2 \stackrel{?}{<} 7^2+8^2\)
\(81 \stackrel{?}{<} 49+64\)
\(81 \stackrel{?}{<} 113\) ✓
Logo, é acutângulo.
Exemplo 2 — Num triângulo acutângulo, \(b=10\), \(c=12\) e \(A=40^\circ\). Calcule a área.
Mostrar solução
Use \( A=\dfrac{bc\sin A}{2} \):
\(A=\dfrac{10\cdot 12\cdot \sin 40^\circ}{2}\)
\(=\dfrac{120\cdot 0{,}642788\ldots}{2}\)
\(=\dfrac{77{,}1346\ldots}{1}\)
\(\approx 77{,}13\ \text{u}^2\).
Atalho trigonométrico prático; veja também triângulo retângulo para revisar razões trigonométricas.
Exercícios de múltipla escolha (com solução em abre/fecha)
1) O triângulo de lados \(6,7,8\) é:
Mostrar solução
Maior lado \(=8\).
\(8^2 \stackrel{?}{<} 6^2+7^2\)
\(64 \stackrel{?}{<} 36+49\)
\(64 \stackrel{?}{<} 85\) ✓
Alternativa C (acutângulo).
2) Em um triângulo acutângulo, \(a=9\), \(b=12\) e \(C=50^\circ\). A área é aproximadamente:
Mostrar solução
\(A=\dfrac{ab\sin C}{2}\)
\(=\dfrac{9\cdot 12\cdot \sin 50^\circ}{2}\)
\(=\dfrac{108\cdot 0{,}7660\ldots}{2}\)
\(=\dfrac{82{,}728\ldots}{2}\)
\(\approx 41{,}36\).
Alternativa B.
3) Para lados \(8,15,c\) com maior lado \(c\), o triângulo é acutângulo se:
Mostrar solução
\(c^2 < 64+225=289\)
\(c < 17\).
Alternativa C.
4) Num triângulo acutângulo, qual afirmação é sempre verdadeira?
Mostrar solução
D. No acutângulo, ortocentro, incentro e circuncentro ficam dentro do triângulo; alturas são internas.
5) Se \(a=10\), \(b=13\), \(c=14\). Classifique-o por ângulos.
Mostrar solução
Maior lado \(=14\).
\(14^2 \stackrel{?}{<} 10^2+13^2\)
\(196 \stackrel{?}{<} 100+169\)
\(196 \stackrel{?}{<} 269\) ✓
Alternativa C.
6) Em um acutângulo, \(b=11\), \(c=12\) e \(A=35^\circ\). O raio da circunferência circunscrita é:
Mostrar solução
\(a^2=b^2+c^2-2bc\cos A\)
\(=121+144-264\cdot 0{,}81915\ldots\)
\(=48{,}75\Rightarrow a\approx 6{,}985\).
\(2R=\dfrac{a}{\sin A}=\dfrac{6{,}985}{\sin35^\circ}\approx 12{,}18\Rightarrow R\approx 6{,}09\).
Alternativa B (≈6,1).
7) No triângulo acutângulo, \(a=9\), \(b=10\), \(C=40^\circ\). A altura relativa a \(c\) é:
Mostrar solução
\(c^2=9^2+10^2-2\cdot9\cdot10\cos40^\circ=43{,}12\Rightarrow c\approx 6{,}57\).
\(h_c=\dfrac{ab\sin C}{c}=\dfrac{9\cdot10\cdot \sin 40^\circ}{6{,}57}\approx \mathbf{8{,}81}\).
Alternativa C (≈8,8).
8) Para \(a=5\), \(b=7\), \(c=8\), a área por Heron é aproximadamente:
Mostrar solução
\(s=\dfrac{5+7+8}{2}=10\).
\(A=\sqrt{10\cdot 5\cdot 3\cdot 2}=\sqrt{300}\approx \mathbf{17{,}32}\).
Alternativa B.
9) Em qualquer acutângulo, qual ponto notável fica fora do triângulo?
Mostrar solução
No acutângulo, todos ficam internos.
Alternativa E.
10) Um triângulo acutângulo tem perímetro 29 com lados \(8\), \(x\) e \(y\) (\(y\) é o maior). Se \(x=9\), qual é \(y\)?
Mostrar solução
\(8+9+y=29\Rightarrow y=12\).
Teste: \(12^2=144<8^2+9^2=145\) ✓ (acutângulo).
Alternativa C.
Quer uma lista maior (com gabarito editável) para sala de aula? Use o Banco de Questões e o pacote ENEM Matemática.
Continue estudando
Triângulo retângulo Triângulo obtusângulo Área de triângulo Pontos notáveis Tipos de triângulos Triângulo equilátero Triângulo escaleno
Para revisar tudo em 1 página (acutângulo × retângulo × obtusângulo), veja os Mapas Mentais de Matemática.
Produtos do blog — destaque
Mapas Mentais de Matemática
Resumos visuais de classificação por ângulos, leis dos cossenos e áreas — perfeito para o tema “acutângulo”.
Quero os Mapas+600 Questões ENEM Comentadas
Centenas de itens envolvendo classificação de triângulos, área por seno e Heron.
Praticar agoraColeção 10 eBooks
Teoria objetiva + exercícios com gabarito (geometria plana completa).
Ver coleçãoBanco de Questões (editáveis)
Monte listas por assunto (acutângulo, retângulo, obtusângulo) para treinos dirigidos.
Acessar bancoCanais Oficiais
Receba novas listas, simulados e artigos diretamente nos canais.
Entrar nos canais