Na figura ao lado há três segmentos consecutivos e não colineares, AB, BC e CA. Juntos, esses segmentos formam um polígono (ou linha poligonal fechada) chamado triângulo. Indicamos o triângulo ABC por ∆ABC.
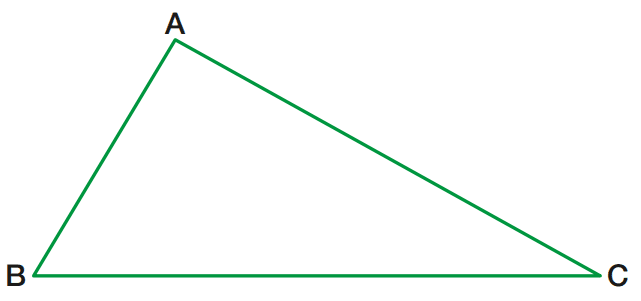
Dados três pontos A, B e C não colineares, chama-se triângulo ABC a reunião dos segmentos AB, BC e CA.
Em um triângulo ABC, os pontos A, B e C são chamados vértices, e os segmentos AB (de medida c), BC (de medida a) e CA (de medida b) são chamados lados.

Os ângulos BAC (ou A), ABˆC (ou B) e ACB (ou C) são chamados ângulos internos do triângulo. Para simplificar a linguagem, é usual dizer:
- o lado a é o oposto ao ângulo A
- o lado b é o oposto ao ângulo B
- o lado c é o oposto ao ângulo C
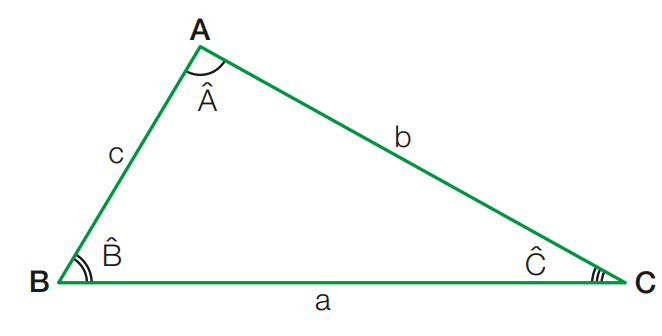
O perímetro de um triângulo, é a soma das medidas dos seus lados. No triângulo ABC, temos:
Perímetro: a + b + c
Classificação de triângulos quanto aos lados
Quando comparamos os lados de um triângulo, três casos podem ocorrer:
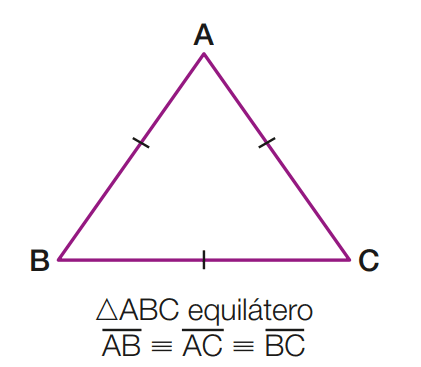
1° caso – Os três lados são congruentes. Nesse caso, o triângulo é chamado de equilátero.
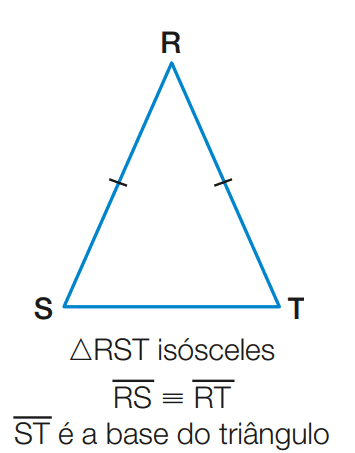
2° caso – Dois lados são congruentes. O outro lado é chamado de base do triângulo. Nesse caso, o triângulo é dito isósceles.
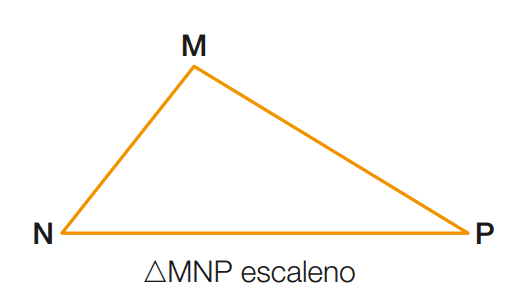
3° caso – Dois lados quaisquer não são congruentes. Nesse caso, o triângulo é dito escaleno.
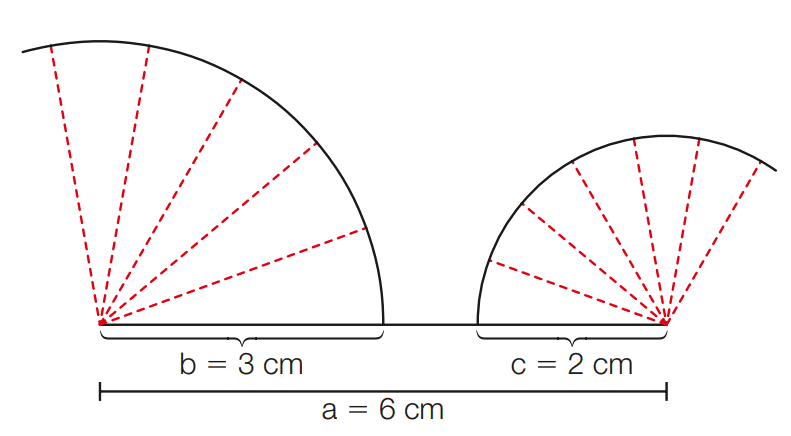
Desigualdade triangular
Se tentássemos construir um triângulo de lados medindo a = 6 cm, b = 3 cm e c = 2 cm, obteríamos a figura ao lado. Os arcos não se cruzam.
Isso significa que não existe triângulo de lados medindo 6 cm, 3 cm e 2 cm.
Por que isso acontece? Esse fato é justificado pela propriedade a seguir:
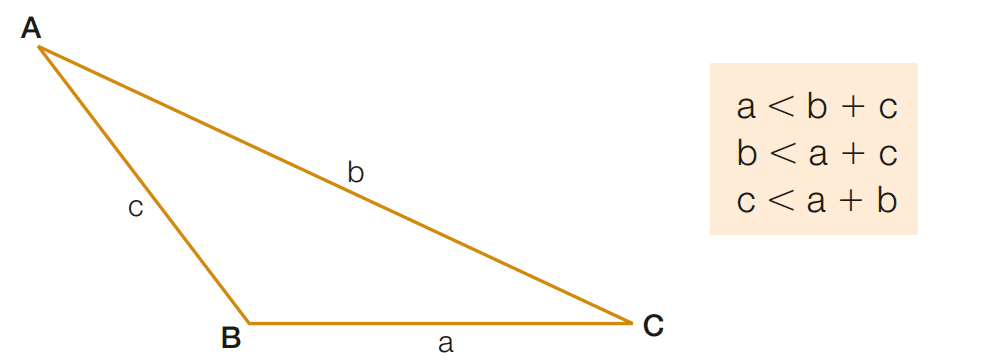
Então, dado o triângulo ABC, em que a é medida do lado BC, b é medida do lado AC e c é medida do lado AB, podemos escrever as seguintes relações:
Em qualquer triângulo, a medida de cada lado é menor que a soma das medidas dos outros dois lados.
Portanto, podemos saber se existe ou não um triângulo de determinadas medidas comparando a maior delas com a soma das outras duas. O triângulo só existirá se a medida do lado maior for menor que a soma das medidas dos outros dois.
Classificação de triângulos quanto aos lados
Quando comparamos os lados de um triângulo, três casos podem ocorrer:
1° caso – Os três lados são congruentes. Nesse caso, o triângulo é chamado de equilátero.

2° caso – Dois lados são congruentes. O outro lado é chamado de base do triângulo. Nesse caso, o triângulo é dito isósceles.

3° caso – Dois lados quaisquer não são congruentes. Nesse caso, o triângulo é dito escaleno.

Propriedade da soma dos ângulos internos de um triângulo
Vamos considerar um triângulo ABC e seus ângulos, Aˆ, Bˆ e Cˆ
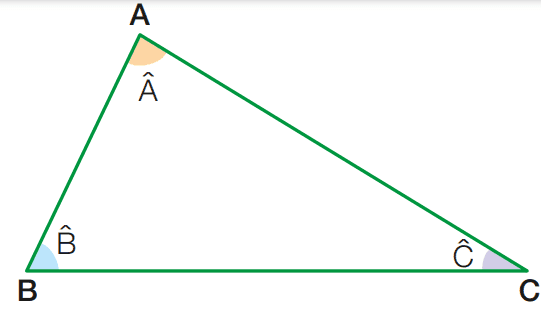
Pelo vértice A, vamos traçar uma reta r paralela ao lado BC e marcar os ângulos 1ˆ e 2ˆ, como abaixo:
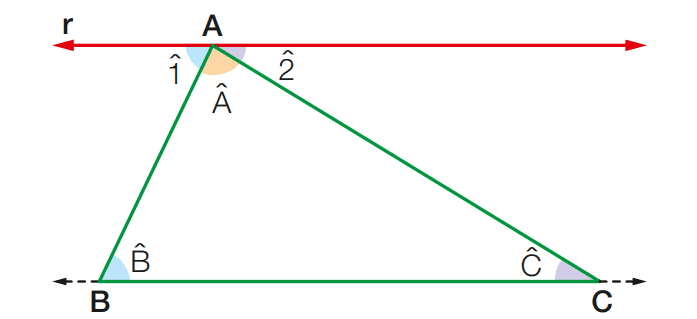
Do paralelismo de r e BC, considerando a transversal AB, decorre que:
1ˆ = Bˆ
Do paralelismo de r e BC, considerando a transversal AC, decorre que:
2ˆ = Cˆ
Substituindo 1ˆ por Bˆ e 2ˆ por Cˆ na figura, temos:
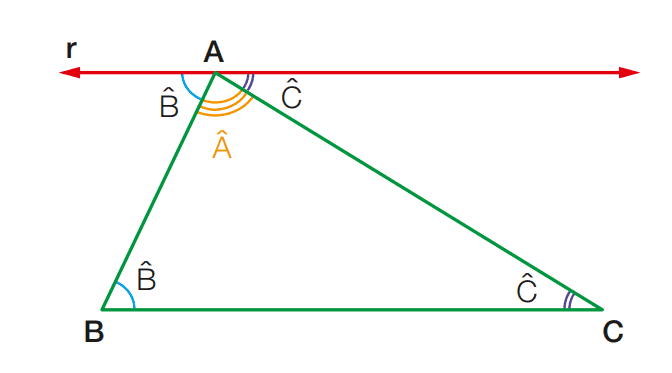
Adicionando as medidas dos ângulos que têm vértice em A, concluímos que:
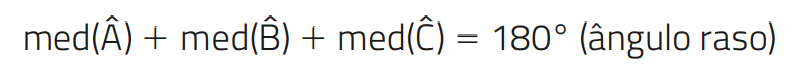
Esse resultado é resumido pela propriedade:
A soma das medidas dos ângulos internos de um triângulo é 180°
Classificação dos triângulos quanto aos ângulos
Os triângulos podem ser classificados em relação às medidas dos ângulos internos. Considerando que a soma das medidas dos ângulos de um triângulo é 180°, podem ocorrer as seguintes situações:
Os três ângulos são agudos. Nesse caso, o triângulo é dito acutângulo.
Por exemplo, o triângulo representado ao lado tem ângulos internos de medidas 50°, 60° e 70°.
Note que: 50° + 60° + 70° = 180°

Um dos ângulos é reto e os outros dois são agudos. Nesse caso, o triângulo é dito retângulo.
Por exemplo, o triângulo representado ao lado tem ângulos internos de medidas 90°, 35° e 55°.
Note que: 90° + 35° + 55° = 180°

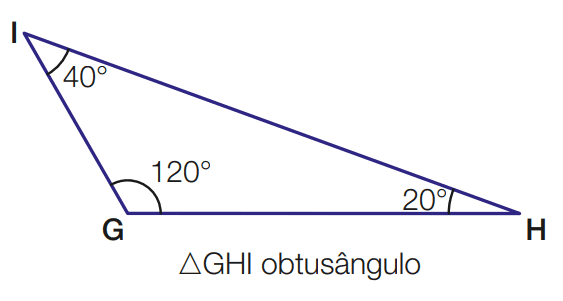
Um dos ângulos é obtuso e os outros dois são agudos. Nesse caso, o triângulo é dito obtusângulo.
Por exemplo, o triângulo representado ao lado tem ângulos internos de medidas 120°, 20° e 40°.
Note que: 120° + 20° + 40° = 180°
Propriedade do ângulo externo de um triângulo
Considere o triângulo ABC representado abaixo:

Vamos prolongar o lado BC do triângulo ABC na extremidade C e tomar um ponto X no prolongamento, de modo que a semirreta CX seja oposta à semirreta CB.
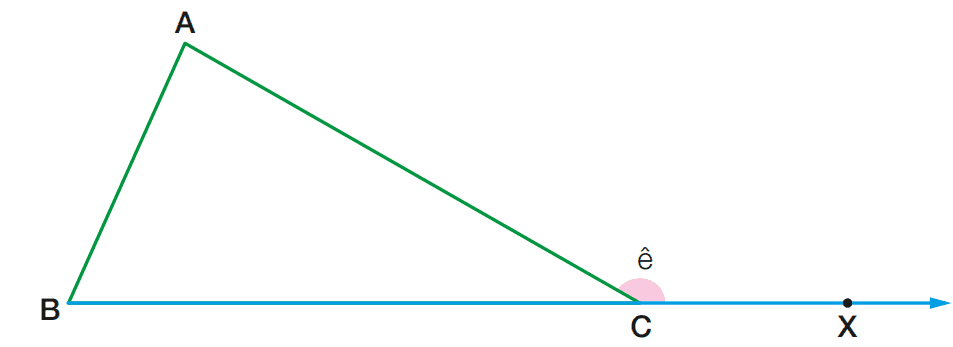
Dizemos que o ângulo ACˆX é um ângulo externo do triângulo ABC.
Observe que o ângulo externo ê = ACˆX é adjacente ao ângulo Cˆ do triângulo. Mas os ângulos Aˆ e Bˆ não são adjacentes ao ângulo externo ê
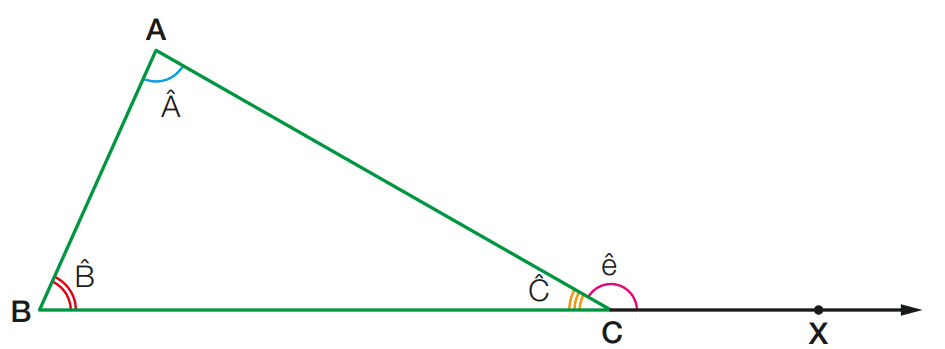
Observe, ainda, que:
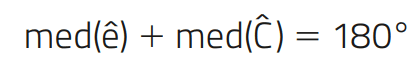
pois eˆ e Cˆ são adjacentes e suplementares
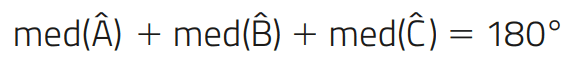
soma dos ângulos internos de um triângulo
Então, temos:
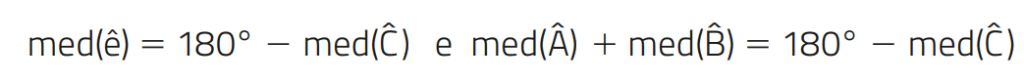
Logo,

Em todo triângulo, qualquer ângulo externo tem medida igual à soma das medidas dos dois ângulos internos não adjacentes a ele.
A geometria é uma área fundamental da matemática, dedicada ao estudo das formas, tamanhos e propriedades de figuras no plano e no espaço.
Lista de Exercícios sobre triângulo com solução
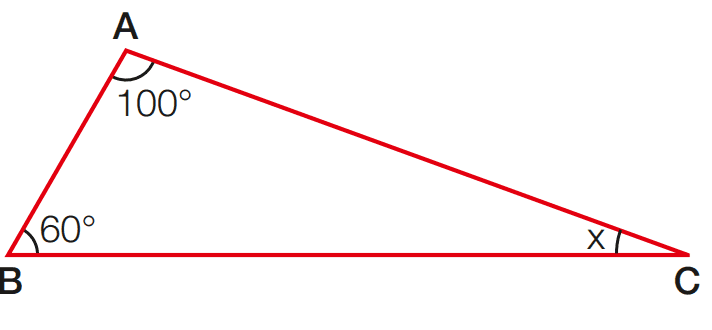
Exercício 1 – Em cada item, calcule o valor de x e classifique o triângulo em relação aos ângulos
a)
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Temos que 100 + 60 + x = 180
x = 180 – 100 – 60 = 20
Resposta: x = 20°; triângulo obtusângulo
[/toggle]
b)
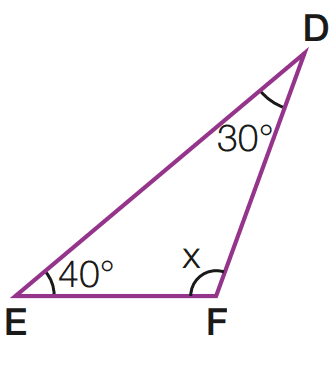
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Temos que 40 + 30 + x = 180
x = 180 – 40 – 30 = 110
x = 110
Resposta: x = 110°; triângulo obtusângulo
[/toggle]
c)

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Temos que 90 + 40 + x = 180
x = 180 – 90 – 40 = 50
x = 50
Resposta: x = 50°; triângulo retângulo
[/toggle]
Exercício 2: Qual é o valor de x?
a)

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Pelo teorema do ângulo externo temos
x = 20 + 30
x = 50°
[/toggle]
b)
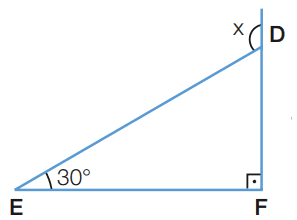
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Pelo teorema do ângulo externo temos:
x = 30 + 90
x = 120°
[/toggle]
c)

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
2x − 10 = x + y
Onde y = 180 − (2x + 10)
E, usando as propriedades dos ângulos e a soma dos ângulos internos de um triângulo (que somam 180), você chegou à seguinte equação:
2x − 10 = x + 180 − (2x + 10)
A partir dessa equação, o desenvolvimento correto leva ao valor final de:
3x = 180 ⟹ x = 60
Portanto, o valor correto de x é, de fato, 60 graus.
[/toggle]
Exercício 3: Calcule a soma x + y + z nos seguintes casos:
a)

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Utilizando suplemento de cada ângulo temos:
180 – x + 180 – y + 180 – z = 180
x – y – z + 540 = 180
x – y – z = 180 – 540
x – y – z = – 360 x(-1)
x + y + z = 360
[/toggle]
b)
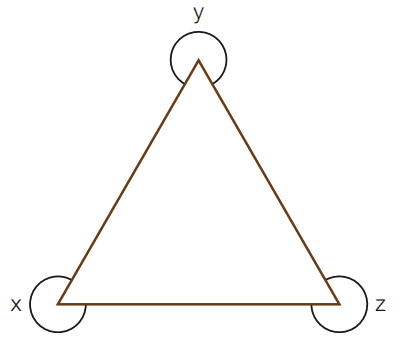
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
360 – x + 360 -y +360 – z = 180
1080 – x – y – z = 180
x – y – z = 180 – 1080
x – y – z = -900
x + y + z = 900
[/toggle]
Exercício 4: Determine os valores de x e y em cada item
a)
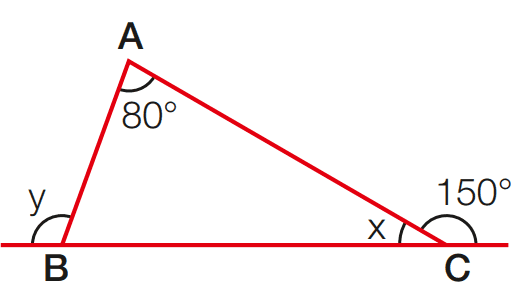
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
x = 180 – 150
x = 30
y = 80 + 30
y = 110
[/toggle]
b)
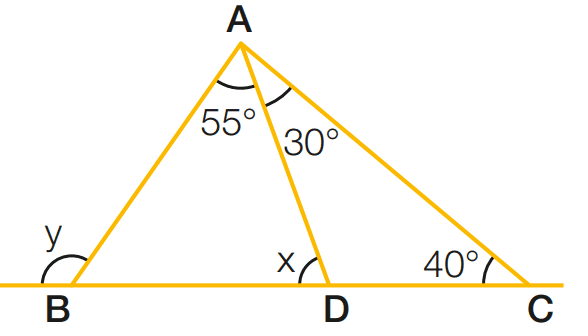
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
x = 30 + 40
x = 70
y = 55 + 70
y = 175
[/toggle]
Exercício 5: Sabendo que r // s, calcule o valor de x.
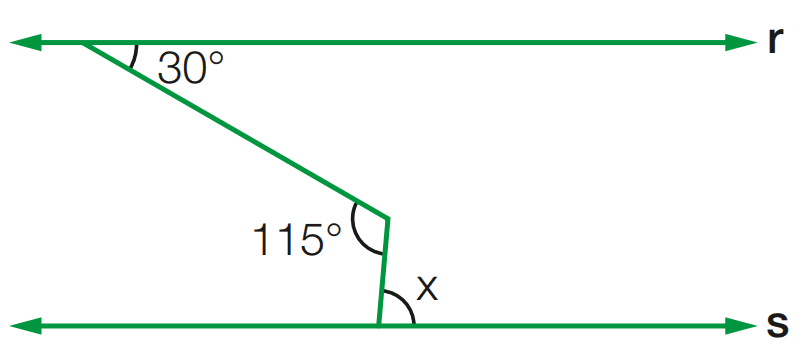
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
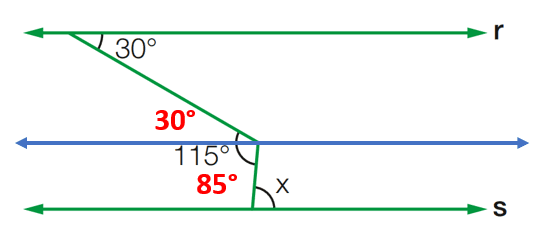
x = 85
[/toggle]
Exercício 6: Na figura, r é paralela a s. Determine a soma x + y.
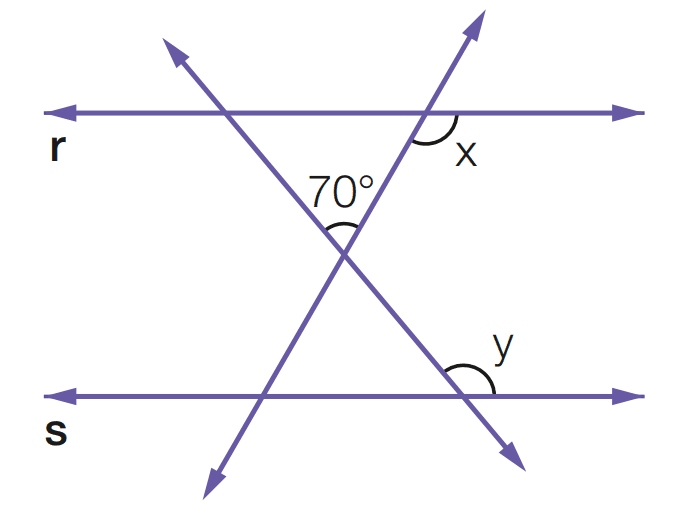
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
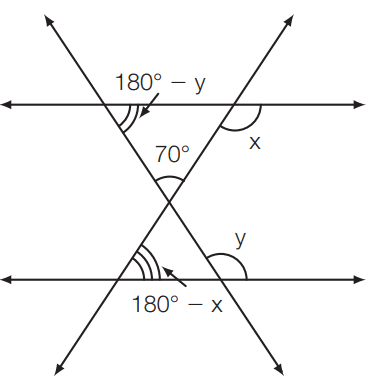
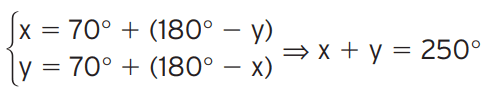
[/toggle]
Exercício 7: Pode-se dizer que existe um triângulo que seja:
a) acutângulo e isósceles?
b) obtusângulo e isósceles?
c) retângulo e isósceles?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
a) Sim.
b) Sim.
c) Sim.
[/toggle]
Exercício 8: O ângulo do vértice de um triângulo isósceles mede 67° 32′ 52”. Calcule as medidas dos ângulos adjacentes à base desse triângulo.
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
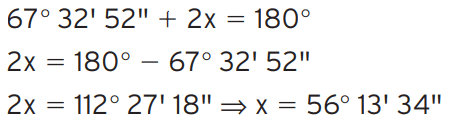
[/toggle]
Exercício 9: Calcule os valores de x e y em cada uma das figuras abaixo.
a)
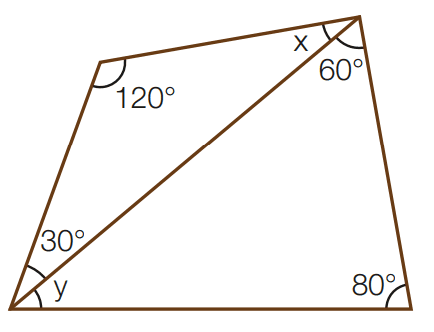
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
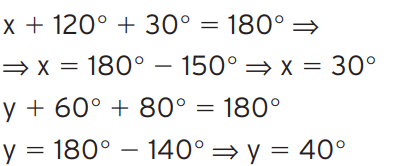
[/toggle]
b)
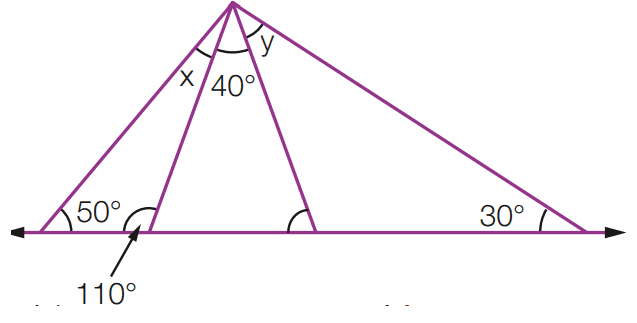
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
Exercício 10: Sabendo que as retas r e s são paralelas, calcule os valores de x, y e z.
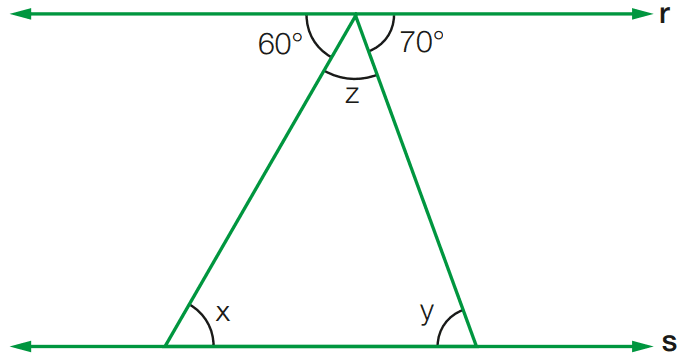
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
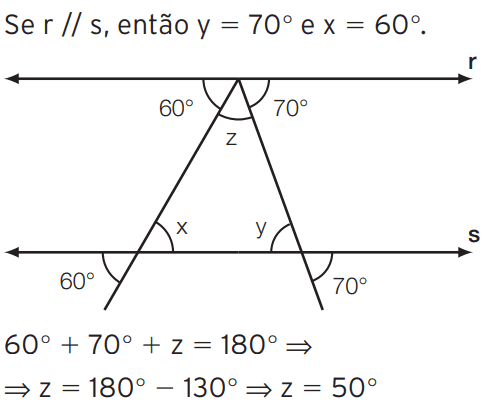
[/toggle]
Exercício 11: Sabendo que r // s, calcule o valor de x.
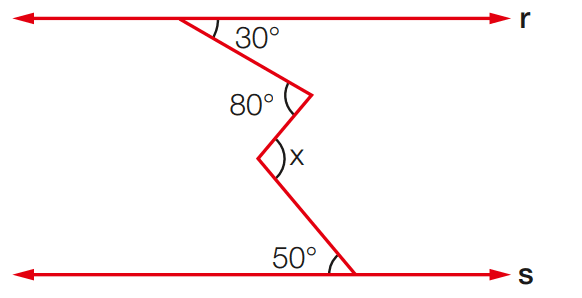
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
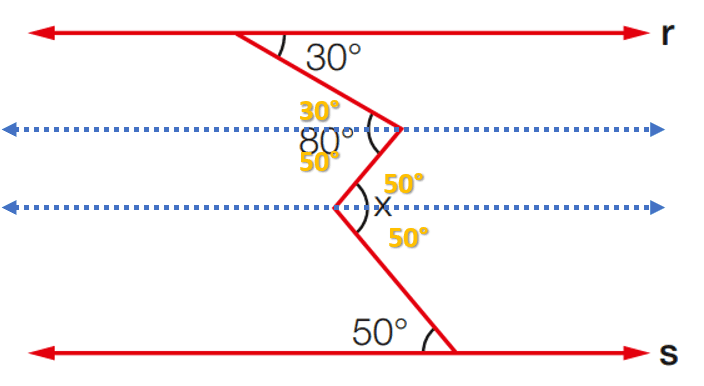
x = 50 + 50
x = 100
[/toggle]
Exercício 12: Sabendo que r // s, calcule os valores de x e y.

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
Exercício 13: Determine o valor de x em cada caso.
a)

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
x = 130 + 40 ⇨ x = 170
[/toggle]
b)

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
180 – 150 = 30
x = 90 + 30 ⇨ x = 120
[/toggle]
c)
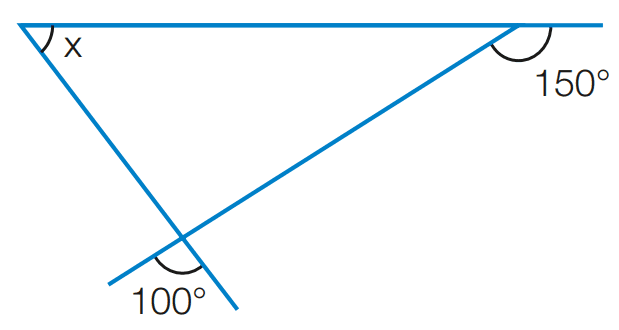
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
180 – 150 = 30
x + 100 + 30 = 180
x = 180 – 100 – 30
x = 50
[/toggle]
d)
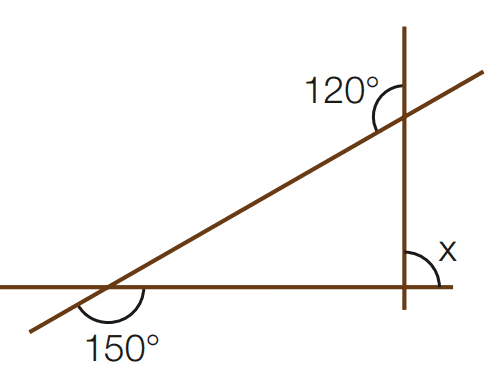
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
180 – 120 = 60
180 – 150 = 30
x = 30 + 60 ⇨ x = 90
[/toggle]
e)
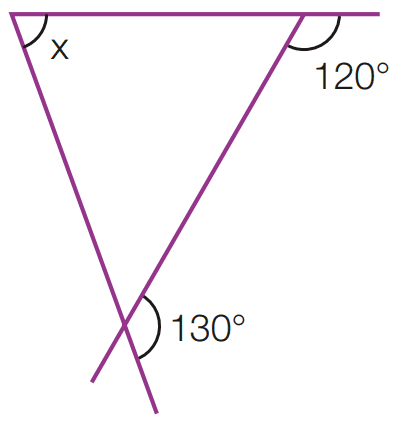
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
180 – 120 = 60
180 – 130 = 50
x + 60 + 50 = 180
x = 180 – 110
x = 70
[/toggle]
Exercício 14: Determine a medida dos ângulos internos de um triângulo, sabendo que os ângulos externos medem, em graus, respectivamente: x, x + 10 e x – 10
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
x + x + 10 + x – 10 = 180
3x = 180
x = 180/3
x = 60
1) x + 10 = 60 + 10 = 70
2) x – 10 = 60 – 10 = 50
3) x = 60
[/toggle]
Exercício 15: Calcule o valor de x na figura abaixo.
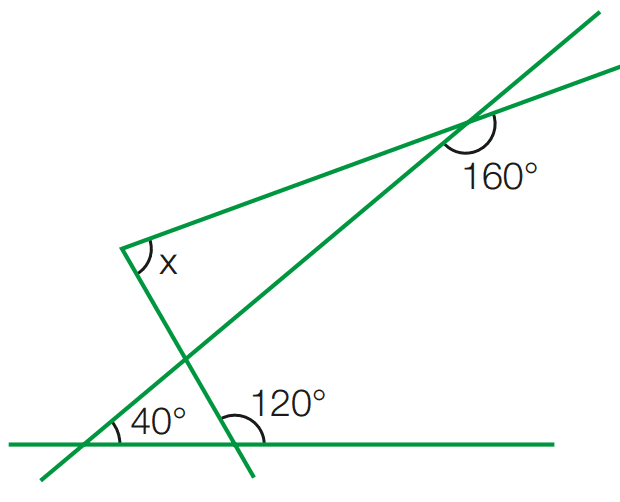
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
180 – 160 = 40
180 – 120 = 60
y + 40 + 60 = 180
y = 180 – 100
y = 80 (ângulo opv)
x + 20 + 80 = 180
x = 180 – 100
x = 80
[/toggle]













