Triângulo Obtusângulo — propriedades, fórmulas (uma por linha), exemplos e exercícios

Um triângulo é obtusângulo quando possui um ângulo interno maior que \(90^\circ\).

O que é um triângulo obtusângulo?

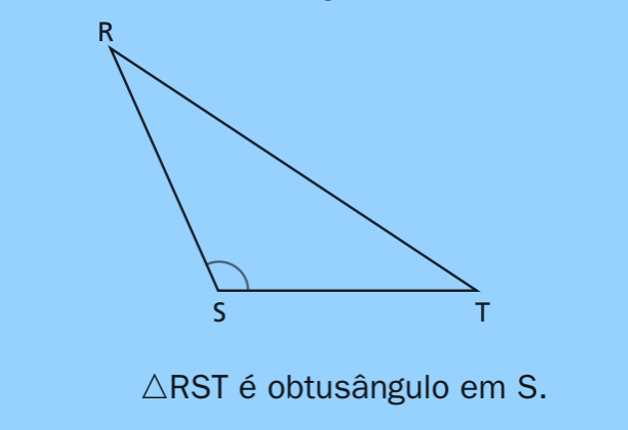
Chamamos de triângulo obtusângulo aquele que tem um ângulo maior que \(90^\circ\) (obtuso) e os demais ângulos agudos. Na classificação por ângulos temos: triângulo acutângulo, triângulo retângulo e triângulo obtusângulo. Para a classificação completa (por lados e ângulos), veja Tipos de Triângulos.

O maior ângulo fica sempre oposto ao maior lado. Se houver um lado bem maior que os outros, suspeite do ângulo oposto como obtuso.

Como reconhecer um triângulo obtusângulo

1) Pelos ângulos

Se \( \max(\angle A,\angle B,\angle C) > 90^\circ \Rightarrow \) obtusângulo.

2) Pelos lados (Pitágoras ao contrário)

Sejam \(a,b,c\) os lados e **\(c\)** o maior (oposto a **\(C\)**). Então:

Obtusângulo ⇔ \( \;c^2 > a^2 + b^2 \). Retângulo ⇔ \( \;c^2 = a^2 + b^2 \) — ver triângulo retângulo. Acutângulo ⇔ \( \;c^2 < a^2 + b^2 \) — ver triângulo acutângulo.

Esse teste deriva da lei dos cossenos e funciona mesmo sem os ângulos.

Propriedades importantes

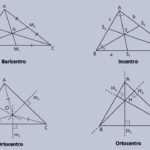
Ortocentro e circuncentro ficam fora do triângulo obtusângulo.
Baricentro (medianas) e incentro (bissetrizes) são internos.
A altura traçada a partir do vértice do ângulo obtuso intercepta a extensão do lado oposto (o pé da altura cai fora do triângulo).
O lado oposto ao ângulo obtuso é o maior lado.

Para revisar os pontos notáveis com figuras, veja Pontos Notáveis do Triângulo. Precisa de um resumo rápido? Use os Mapas Mentais.

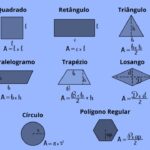
Fórmulas úteis (uma por linha e coloridas)

Lei dos cossenos: \( \displaystyle c^2=a^2+b^2-2ab\cos C \) (com \(c\) oposto a \(C\)). Critério “obtuso” (maior lado \(c\)): \( \displaystyle c^2 > a^2+b^2 \) ⇔ \(C>90^\circ\). Área pela trigonometria: \( \displaystyle A=\frac{ab\sin C}{2}=\frac{bc\sin A}{2}=\frac{ca\sin B}{2} \). Área (base–altura): \( \displaystyle A=\frac{b\cdot h_b}{2} \) — quando \(b\) se opõe ao ângulo obtuso, \(h_b\) é medida até a extensão de \(b\). Fórmula de Heron: \( \displaystyle A=\sqrt{\,s(s-a)(s-b)(s-c)\,} \), com \( s=\frac{a+b+c}{2} \). Alturas: \( \displaystyle h_a=\frac{2A}{a},\; h_b=\frac{2A}{b},\; h_c=\frac{2A}{c} \). Raio da circunscrita e da inscrita: \( \displaystyle R=\frac{a}{2\sin A}=\frac{b}{2\sin B}=\frac{c}{2\sin C},\quad r=\frac{A}{s} \).

Domine áreas (Heron, base–altura, seno) em Área de Triângulo. Relacione também com triângulo equilátero e triângulo escaleno.

Exemplos resolvidos (passo a passo vertical)

Exemplo 1 — Classifique por ângulos o triângulo de lados \(7\), \(10\), \(13\).

Mostrar solução

Maior lado: \(13\).

\(13^2 \stackrel{?}{>} 7^2+10^2\)
\(169 \stackrel{?}{>} 49+100\)
\(169 \stackrel{?}{>} 149\) ✓

Logo, é obtusângulo.

Exemplo 2 — Em um triângulo, \(a=9\), \(b=12\) e o ângulo compreendido é \(C=120^\circ\). Calcule \(c\) e a área.

Mostrar solução

Lado \(c\) (lei dos cossenos; \(\cos 120^\circ=-\tfrac12\)):

\(c^2=a^2+b^2-2ab\cos C\)
\(=9^2+12^2-2\cdot 9\cdot 12\cdot (-\tfrac12)\)
\(=81+144+108\)
\(=333\Rightarrow c=\sqrt{333}\approx 18{,}25\).

Área ( \(\sin 120^\circ=\tfrac{\sqrt3}{2}\approx 0{,}8660\) ):

\(A=\dfrac{ab\sin C}{2}\)
\(=\dfrac{9\cdot 12\cdot 0{,}8660}{2}\)
\(=\dfrac{93{,}53}{2}\)
\(\approx 46{,}76\ \text{u}^2\).

Exercícios de múltipla escolha (com solução em abre/fecha)

1) O triângulo com lados \(5,6,8\) é:

A) Retângulo B) Obtusângulo C) Acutângulo D) Equilátero E) Isósceles

Mostrar solução

Maior lado \(=8\).

\(8^2 \stackrel{?}{>} 5^2+6^2\)
\(64 \stackrel{?}{>} 25+36\)
\(64 \stackrel{?}{>} 61\) ✓

Alternativa B.

2) Seja \(c\) o maior lado. O triângulo é obtusângulo se e somente se:

A) \(c^2=a^2+b^2\) B) \(c^2>a^2+b^2\) C) \(c^2<a^2+b^2\) D) \(c=a+b\) E) \(c\le a\)

Mostrar solução

Critério de Pitágoras ao contrário.

Alternativa B.

3) Para formar um obtusângulo com maior lado \(c=13\) e outro lado \(a=5\), o terceiro lado \(b\) deve satisfazer:

A) \(b\le 8\) B) \(8<b<12\) C) \(b\ge 12\) D) \(b>13\) E) \(2<b<8\)

Mostrar solução

Desigualdade triangular: \(13<5+b\Rightarrow b>8\) e \(b<18\).

Obtuso no maior lado: \(13^2>5^2+b^2\Rightarrow b^2<144\Rightarrow b<12\).

Logo \(8<b<12\). Alternativa B.

4) No triângulo obtusângulo, quais pontos notáveis ficam fora do triângulo?

A) Baricentro B) Incentro C) Ortocentro D) Circuncentro E) Ortocentro e circuncentro

Mostrar solução

Ambos são externos. Alternativa E.

5) Dado \(a=9\), \(b=12\) e \(C=120^\circ\). O valor aproximado de \(c\) é:

A) 16,0 B) 17,3 C) 18,3 D) 19,0 E) 20,0

Mostrar solução

\(c^2=9^2+12^2-2\cdot 9\cdot 12\cos120^\circ\)
\(=81+144+108\)
\(=333\Rightarrow c=\sqrt{333}\approx \mathbf{18{,}25}\).

Alternativa C.

6) Com os dados do exercício anterior, a área é aproximadamente:

A) 36,5 B) 42,0 C) 46,8 D) 51,0 E) 60,0

Mostrar solução

\(A=\dfrac{ab\sin C}{2}\)
\(=\dfrac{9\cdot 12\cdot \sin120^\circ}{2}\)
\(=\dfrac{108\cdot 0{,}8660}{2}\)
\(=\dfrac{93{,}53}{2}\)
\(\approx \mathbf{46{,}76}\).

Alternativa C.

7) No obtusângulo, o pé da altura relativa ao lado oposto ao ângulo obtuso cai:

A) Dentro do segmento B) No ponto médio C) No vértice D) Fora do segmento (na extensão) E) Sobre a circunferência inscrita

Mostrar solução

Na extensão do lado. Alternativa D.

8) Em um triângulo com lados \(7,9,13\), qual ângulo é obtuso?

A) O oposto a 7 B) O oposto a 9 C) O oposto a 13 D) Todos E) Nenhum

Mostrar solução

O maior ângulo é oposto ao maior lado. Alternativa C.

9) Onde fica o circuncentro de um triângulo obtusângulo?

A) Dentro B) No lado C) No vértice D) Fora E) No baricentro

Mostrar solução

Fora do triângulo. Alternativa D.

10) Para lados \(11\), \(x\) e \(13\) (sendo \(13\) o maior), para que o triângulo seja obtusângulo com ângulo oposto a \(13\), \(x\) deve satisfazer:

A) \(x\ge 13\) B) \(x\le 2\) C) \(2<x<6{,}93\) D) \(6{,}93\le x<13\) E) \(x>13\)

Mostrar solução

Triangular: \(13<11+x\Rightarrow x>2\) e \(x<13\).

Obtuso no maior: \(13^2>11^2+x^2\Rightarrow x^2<48\Rightarrow x<\sqrt{48}\approx 6{,}93\).

Logo \(2<x<6{,}93\). Alternativa C.

Quer listas maiores (com gabarito editável)? Use o Banco de Questões e treine com o pacote ENEM Matemática.