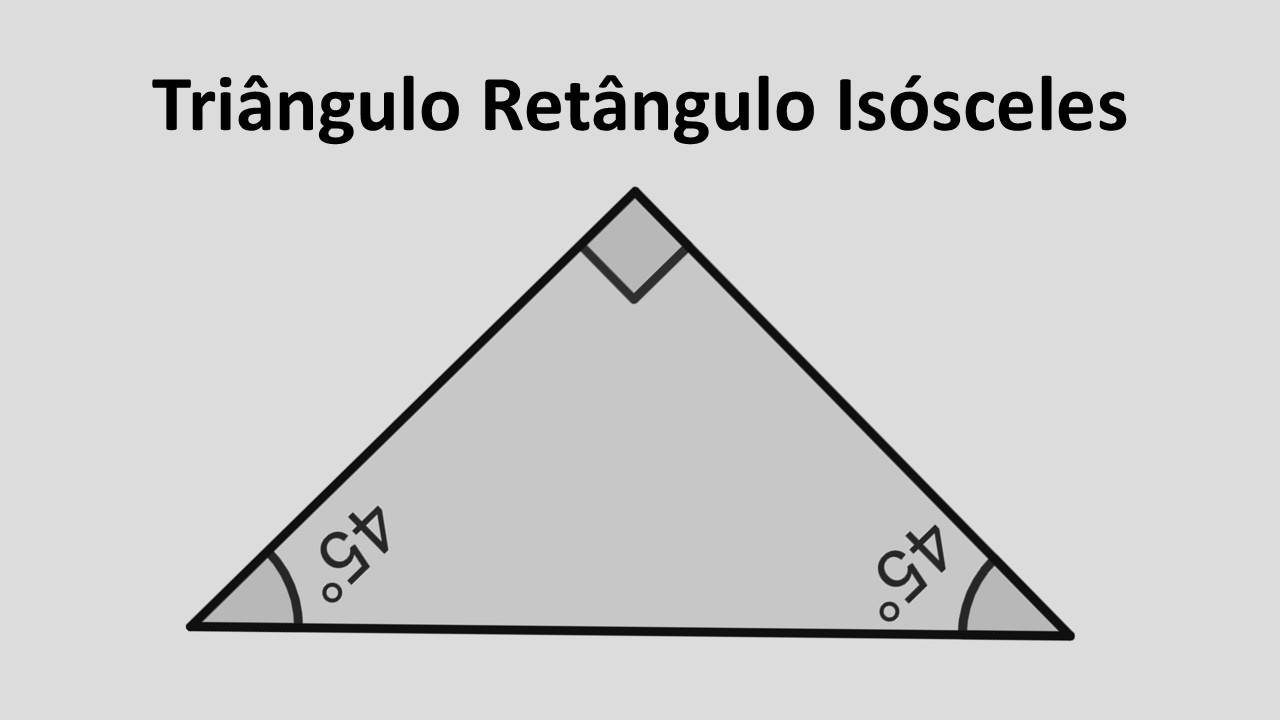
Triângulo Retângulo Isósceles (45°-45°-90°)
SEO discreto: triângulo retângulo isósceles, 45-45-90, triângulos retângulos, triângulo isósceles.
Definição e propriedades básicas
- É um triângulo retângulo com dois lados iguais (os catetos). Logo, os ângulos agudos são \(45^\circ\) e \(45^\circ\).
- Pelo Teorema de Pitágoras, se o cateto vale \(a\), então a hipotenusa é \(c=a\sqrt2\).
- Razões trigonométricas: \(\sin45^\circ=\cos45^\circ=\dfrac{\sqrt2}{2}\) e \(\tan45^\circ=1\).
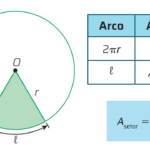
- Raios: incírculo \(r=\dfrac{a+a-c}{2}=\dfrac{a(2-\sqrt2)}{2}\); circunferência circunscrita \(R=\dfrac{c}{2}=\dfrac{a\sqrt2}{2}=\dfrac{a}{\sqrt2}\).
Para revisar fundamentos, veja triângulo retângulo e triângulo isósceles.
Fórmulas essenciais (uma por linha)
Outras relações úteis de triângulos: área de triângulo, pontos notáveis, incírculo e circunscrita.
Exemplos resolvidos (passo a passo vertical)
Exemplo 1 — Dado o cateto \(a=6\). Calcule \(c\), \(A\) e \(P\).
Mostrar solução
\(c=a\sqrt2\)
\(=6\sqrt2\)
\(A=\dfrac{a^2}{2}\)
\(=\dfrac{36}{2}\)
\(=18\)
\(P=2a+c\)
\(=12+6\sqrt2\).
Exemplo 2 — A hipotenusa mede \(c=10\). Determine \(a\), \(A\) e \(r\).
Mostrar solução
\(a=\dfrac{c}{\sqrt2}\)
\(=\dfrac{10}{\sqrt2}\)
\(=5\sqrt2\approx 7{,}071\)
\(A=\dfrac{a^2}{2}\)
\(=\dfrac{(5\sqrt2)^2}{2}\)
\(=\dfrac{50}{2}\)
\(=25\)
\(r=\dfrac{2a-c}{2}\)
\(=\dfrac{2\cdot 5\sqrt2-10}{2}\)
\(=\dfrac{10\sqrt2-10}{2}\)
\(=5(\sqrt2-1)\approx 2{,}071\).
Exemplo 3 — A área vale \(A=32\). Encontre \(a\) e \(c\).
Mostrar solução
\(A=\dfrac{a^2}{2}\Rightarrow a^2=2A\)
\(=64\Rightarrow a=8\)
\(c=a\sqrt2\)
\(=8\sqrt2\).
Exercícios de múltipla escolha (com solução em abre/fecha)
1) No triângulo retângulo isósceles com cateto \(a=5\), a hipotenusa é:
Mostrar solução
\(c=a\sqrt2=5\sqrt2\). Alternativa C.
2) Se \(c=12\sqrt2\), então o cateto \(a\) vale:
Mostrar solução
\(a=c/\sqrt2=12\sqrt2/\sqrt2=12\). Alternativa B.
3) A área para \(a=9\) é:
Mostrar solução
\(A=a^2/2=81/2=40{,}5\). Alternativa C.
4) O perímetro quando \(a=7\) é (aprox.):
Mostrar solução
\(P=2a+a\sqrt2=14+7\sqrt2\approx 14+9{,}899=23{,}899\approx 23{,}9\). Alternativa C.
5) O raio do incírculo para \(a=8\) é (aprox.):
Mostrar solução
\(r=a(2-\sqrt2)/2=8\cdot(2-1{,}4142)/2\approx 8\cdot 0{,}5858/2\approx 2{,}343\). Alternativa C.
6) Para \(a=10\), o raio \(R\) da circunferência circunscrita é:
Mostrar solução
\(R=c/2=(a\sqrt2)/2=10\sqrt2/2=5\sqrt2\). Alternativa D.
7) Se \(A\) é um dos ângulos agudos, então:
Mostrar solução
No 45°-45°-90°, \(\sin45^\circ=\cos45^\circ=\sqrt2/2\). Alternativa C.
8) Um quadrado tem lado \(a\). A diagonal é:
Mostrar solução
A diagonal do quadrado forma um triângulo retângulo isósceles com catetos \(a\). Logo, \(d=a\sqrt2\). Alternativa B.
9) Se a hipotenusa mede \(14\), então o cateto é (aprox.):
Mostrar solução
\(a=c/\sqrt2=14/\sqrt2=7\sqrt2\approx 9{,}899\). Alternativa B.
10) Qual afirmação é verdadeira?
Mostrar solução
Definição principal: \(c=a\sqrt2\). Alternativa C.
Continue estudando
Triângulo retângulo Triângulo isósceles Triângulo equilátero Triângulo escaleno Tipos de triângulos Incírculo e circunscrita Área de triângulo Pontos notáveis Triângulo acutângulo Triângulo obtusângulo
Materiais recomendados
Mapas Mentais de Matemática
Inclui o 45-45-90: \(c=a\sqrt2\), \(A=a^2/2\), \(P=a(2+\sqrt2)\) e muito mais.
Quero os Mapas+600 Questões ENEM Matemática
Pratique triângulos retângulos, isósceles e aplicações com gabarito comentado.
Praticar agoraColeção 10 eBooks
Teoria objetiva + listas resolvidas (geometria plana e trigonometria).
Ver coleçãoBanco de Questões
Monte listas por assunto — perfeito para treinar 45-45-90.
Acessar bancoCanais Oficiais
Drops diários com fórmulas e questões sobre triângulos.
Entrar nos canais