Triângulos Notáveis: Medidas Exatas e Aproximadas
Como reconhecer e usar as razões dos triângulos 30°–60°–90°, 45°–45°–90° e pares aproximados frequentes para resolver problemas de geometria, semelhança e trigonometria.
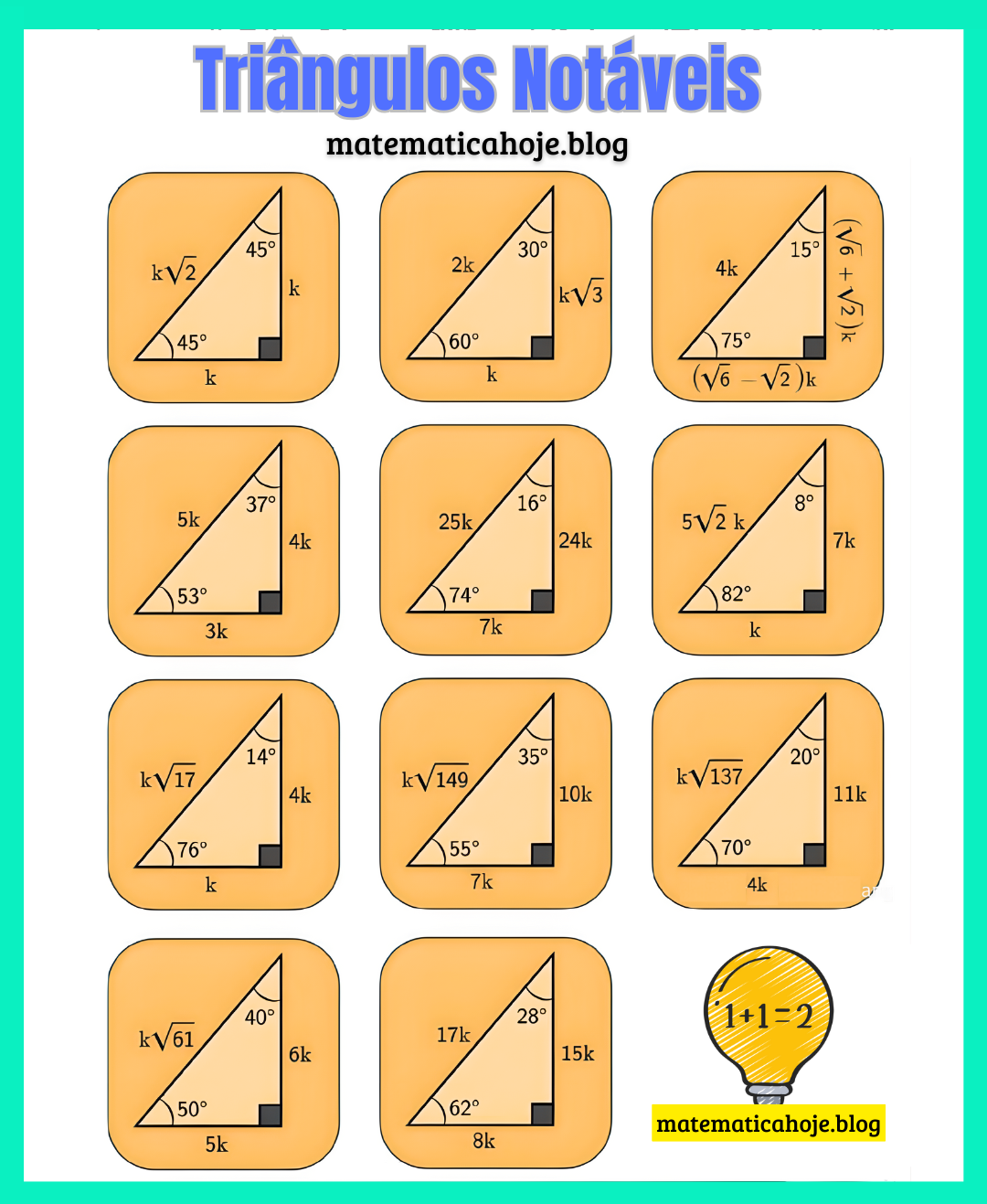
O que são Triângulos Notáveis
Chamamos de triângulos notáveis aqueles cujos ângulos e razões entre lados são bem conhecidos. Eles aparecem em questões de semelhança, trigonometria e geometria analítica, facilitando cálculos e comparações.
- Exatos: 45°–45°–90° e 30°–60°–90° (razões com raízes exatas).
- Aproximados: pares como 37°–53°, 16°–74°, 8°–82° etc., usados para estimativas rápidas.
Triângulos Notáveis Exatos
1) 45°–45°–90° (Isósceles Retângulo)
\( \text{Cateto} = k,\ \text{Cateto} = k,\ \text{Hipotenusa} = k\sqrt{2} \)
Razão: 1 : 1 : √2
2) 30°–60°–90°
\( \text{Cateto oposto a }30° = k,\ \text{Cateto oposto a }60° = k\sqrt{3},\ \text{Hipotenusa} = 2k \)
Razão: 1 : √3 : 2
Triângulos Notáveis Aproximados
Alguns ângulos aparecem com frequência e podem ser aproximados por razões simples:
- 37°–53°: proporções \(3k : 4k : 5k\)
- 16°–74°: \(7k : 24k : 25k\)
- 8°–82°: \(7k : 5\sqrt{2}k : 7k\)
- 14°–76°: \(k : 4k : k\sqrt{17}\)
- 35°–55°: \(7k : 10k : k\sqrt{149}\)
- 20°–70°: \(4k : 11k : k\sqrt{137}\)
- 40°–50°: \(5k : 6k : k\sqrt{61}\)
- 28°–62°: \(8k : 15k : 17k\)
Quando usar cada tipo
- Exatos: quando o problema exige precisão ou envolve trigonometria pura.
- Aproximados: para estimativas, escala e provas práticas.
Exemplo 1 — 45°–45°–90°
Enunciado: Em um triângulo retângulo isósceles, o cateto mede 9 cm. Calcule a hipotenusa.
Ver solução
\( h = 9\sqrt{2} \) \( h = 9 \times 1{,}4142 = 12{,}73\text{ cm} \) Resposta: \( 9\sqrt{2}\text{ cm} \)
Exemplo 2 — 30°–60°–90°
Enunciado: Em um triângulo 30°–60°–90°, a hipotenusa mede 18 cm. Determine os catetos.
Ver solução
\( 2k = 18 \Rightarrow k = 9 \) Cateto(30°) = 9 Cateto(60°) = \(9\sqrt{3}\)
Exemplo 3 — Aproximado 37°–53° (3–4–5)
Enunciado: Uma escada encosta na parede formando aproximadamente 53° com o chão. A base afastada é 3 m. Estime o comprimento da escada.
Ver solução
\( 3k = 3 \Rightarrow k = 1 \) Hipotenusa = \(5k = 5\text{ m}\)
Resposta aproximada: 5 m.
Exercícios Propostos
1) Discursivo — 30°–60°–90°
Num triângulo retângulo, o ângulo agudo menor mede 30° e a hipotenusa mede 12 cm. Calcule os catetos.
Mostrar solução
\( 2k = 12 \Rightarrow k = 6 \) Cateto(30°) = 6 Cateto(60°) = \(6\sqrt{3}\)
2) Discursivo — 45°–45°–90°
Um quadrado tem diagonal \(10\sqrt{2}\text{ cm}\). Encontre a medida do lado.
Mostrar solução
Hipotenusa = L√2 \(10\sqrt{2} = L\sqrt{2} \Rightarrow L = 10\text{ cm}\)
3) Múltipla Escolha — Aproximado 3–4–5
Um terreno retangular precisa de um escoramento em diagonal. A base mede 12 m e a altura 16 m. A diagonal é aproximadamente:
- 18 m
- 20 m
- 22 m
- 24 m
Ver gabarito
\(12:16:20 \sim 3:4:5\) Diagonal = \(5 \times 4 = 20\text{ m}\) Resposta: B
4) Múltipla Escolha — 30°–60°–90°
No triângulo 30°–60°–90°, o cateto oposto a 30° mede 8 cm. A hipotenusa mede:
- 8 cm
- 8√2 cm
- 12 cm
- 16 cm
Ver gabarito
\(k = 8 \Rightarrow \text{Hipotenusa} = 2k = 16\) Resposta: D
5) Desafio — 45°–45°–90°
Um triângulo isósceles retângulo tem perímetro \(20 + 10\sqrt{2}\) cm. Encontre o cateto.
Mostrar solução
\(P = 2k + k\sqrt{2} = 20 + 10\sqrt{2}\) \(k = 10\) Cateto = 10 cm.
Conclusão
Conhecer os triângulos notáveis — exatos e aproximados — permite resolver problemas com rapidez e precisão. Sempre que identificar ângulos 30°–60°–90° ou 45°–45°–90°, aplique suas razões. Em estimativas, use os pares aproximados baseados em triângulos pitagóricos como 3–4–5, 5–12–13 e 8–15–17.
Links do Blog Matemática Hoje
- Mapas Mentais de Matemática
- ENEM Matemática
- 10 eBooks de Matemática
- Banco de Questões de Matemática
- eBook Gratuito de Fórmulas Matemáticas
Convite Final
📲 Baixe grátis o eBook de Fórmulas de Matemática e receba materiais exclusivos no canal do WhatsApp do Matemática Hoje.













