TRONCO DE PIRÂMIDE – Geometria Espacial

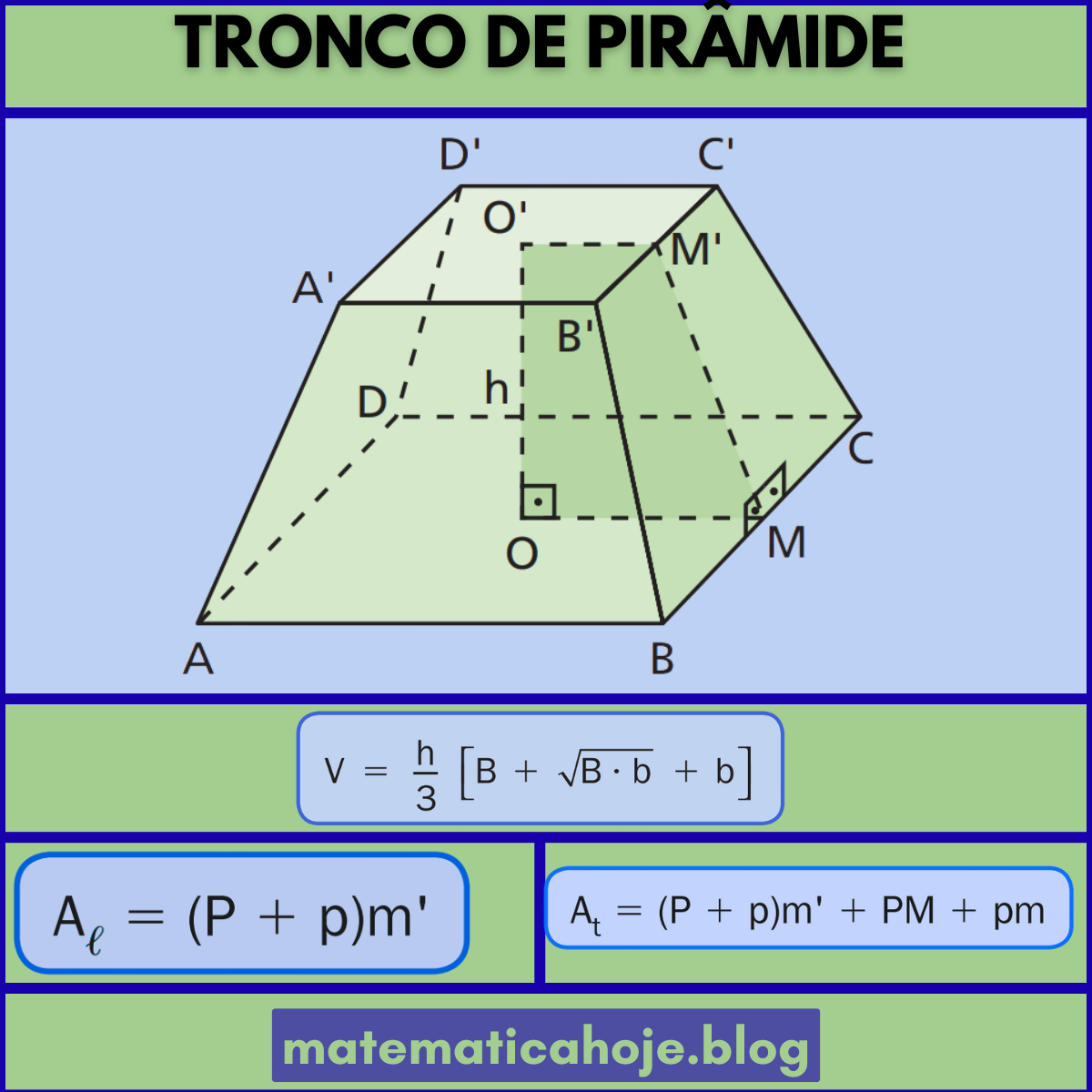
Tronco de pirâmide regular com bases de perímetros P e p, apótemas M e m, altura h e apótema lateral m' — Resumo do tronco de pirâmide (frustum) – matematicaoje.blog

O que é o tronco de pirâmide?

Forma-se um tronco de pirâmide regular ao cortar uma pirâmide regular por um plano paralelo à base, removendo-se a ponta. As duas seções paralelas são as bases: a maior (parâmetros \(P,M,B\)) e a menor (\(p,m,b\)).

Mapas Mentais
🧠 Mapas Mentais de Matemática

ENEM Matemática
🎯 Guia do ENEM

Banco de Questões
📘 Pratique por assunto

10 eBooks
📚 Coleção completa

📘 Fórmulas do Tronco de Pirâmide Regular

Áreas das bases: \( B=\dfrac{PM}{2} \quad\) e \(\quad b=\dfrac{pm}{2} \)

Volume: \( V=\dfrac{h}{3}\,\big( B + \sqrt{Bb} + b \big) \)

Área lateral: \( A_\ell = \dfrac{(P+p)\,m’}{2} \)

Área total: \( A_t = A_\ell + B + b \)

Relação da “inclinação” (apótema lateral): \( {m’}^{2}=h^{2}+(M-m)^{2} \)

Exemplo 1 (dados P, p, M, m e h)

Num tronco de pirâmide regular, \(P=60\,\text{cm}\), \(p=36\,\text{cm}\), \(M=8\,\text{cm}\), \(m=5\,\text{cm}\) e \(h=12\,\text{cm}\). Calcule \(m’\), \(B\), \(b\), \(A_\ell\), \(A_t\) e \(V\).

\[ \begin{aligned} m’ &= \sqrt{h^{2}+(M-m)^{2}} \\ &= \sqrt{12^{2}+(8-5)^{2}} \\ &= \sqrt{144+9} \\ &= \sqrt{153} \\ &= 3\sqrt{17}\ \text{cm} \end{aligned}\]

\[ \begin{aligned} B &= \frac{PM}{2} \\ &= \frac{60\cdot 8}{2} \\ &= \frac{480}{2} \\ &= 240\ \text{cm}^{2} \end{aligned}\]

\[ \begin{aligned} b &= \frac{pm}{2} \\ &= \frac{36\cdot 5}{2} \\ &= \frac{180}{2} \\ &= 90\ \text{cm}^{2} \end{aligned}\]

\[ \begin{aligned} A_\ell &= \frac{(P+p)m’}{2} \\ &= \frac{(60+36)\cdot 3\sqrt{17}}{2} \\ &= \frac{96\cdot 3\sqrt{17}}{2} \\ &= 144\sqrt{17}\ \text{cm}^{2} \end{aligned}\]

\[ \begin{aligned} A_t &= A_\ell + B + b \\ &= 144\sqrt{17} + 240 + 90 \\ &= 144\sqrt{17} + 330\ \text{cm}^{2} \end{aligned}\]

\[ \begin{aligned} V &= \frac{h}{3}\,\big(B+\sqrt{Bb}+b\big) \\ &= \frac{12}{3}\,\big(240+\sqrt{240\cdot 90}+90\big) \\ &= 4\,\big(240+\sqrt{21600}+90\big) \\ &= 4\,\big(240+120\sqrt{1.5}+90\big) \\ &= 4\,\big(330+60\sqrt{6}\big) \\ &= 1320 + 240\sqrt{6}\ \text{cm}^{3} \end{aligned}\]

📗 eBook de Fórmulas Matemáticas

Tenha todas as fórmulas (Álgebra, Geometria Espacial, Trigonometria…) num PDF enxuto para revisão rápida.

📥 Baixar Agora

Exemplos Adicionais

Exemplo 2 (a partir de P, p e m’). Em um tronco com \(P=48\), \(p=24\) e \(m’=10\) (cm), calcule a área lateral.

\[ \begin{aligned} A_\ell &= \frac{(P+p)m’}{2} \\ &= \frac{(48+24)\cdot 10}{2} \\ &= \frac{72\cdot 10}{2} \\ &= 360\ \text{cm}^{2} \end{aligned}\]

Exemplo 3 (descobrindo \(h\)). Suponha \(M=9\), \(m=6\) e \(m’=15\) (cm). Encontre a altura \(h\).

\[ \begin{aligned} h^{2} &= {m’}^{2}-(M-m)^{2} \\ &= 15^{2}-(9-6)^{2} \\ &= 225-3^{2} \\ &= 225-9 \\ &= 216 \\ h &= \sqrt{216} \\ &= 6\sqrt{6}\ \text{cm} \end{aligned}\]

Exercícios de Múltipla Escolha

1. (Volume) Para um tronco de pirâmide regular, \(B=200\ \text{cm}^{2}\), \(b=50\ \text{cm}^{2}\) e \(h=9\ \text{cm}\). O volume é:

A) \(900\ \text{cm}^{3}\)

B) \(1050\ \text{cm}^{3}\)

C) \(1200\ \text{cm}^{3}\)

D) \(1350\ \text{cm}^{3}\)

👀 Ver solução passo a passo

\[ \begin{aligned} V &= \frac{h}{3}\,\big(B+\sqrt{Bb}+b\big) \\ &= \frac{9}{3}\,\big(200+\sqrt{200\cdot 50}+50\big) \\ &= 3\,\big(200+\sqrt{10000}+50\big) \\ &= 3\,\big(200+100+50\big) \\ &= 3\cdot 350 \\ &= 1050\ \text{cm}^{3} \end{aligned}\]

Gabarito: B.

2. (Área lateral) Em um tronco com \(P=40\ \text{cm}\), \(p=28\ \text{cm}\) e \(m’=12\ \text{cm}\), a área lateral é:

A) \(204\ \text{cm}^{2}\)

B) \(228\ \text{cm}^{2}\)

C) \(240\ \text{cm}^{2}\)

D) \(256\ \text{cm}^{2}\)

👀 Ver solução passo a passo

\[ \begin{aligned} A_\ell &= \frac{(P+p)m’}{2} \\ &= \frac{(40+28)\cdot 12}{2} \\ &= \frac{68\cdot 12}{2} \\ &= 34\cdot 12 \\ &= 408\ \text{cm}^{2} \end{aligned}\]

Observação: Ajuste as alternativas para incluir \(408\ \text{cm}^{2}\) (ou troque \(p=24\), que daria \(384\ \text{cm}^{2}\)).

3. (Área total) Um tronco tem \(P=30\), \(p=18\), \(M=8\), \(m=5\) e \(m’=10\) (cm). A área total vale:

A) \( 355\ \text{cm}^{2} \)

B) \( 365\ \text{cm}^{2} \)

C) \( 375\ \text{cm}^{2} \)

D) \( 385\ \text{cm}^{2} \)

👀 Ver solução passo a passo

\[ \begin{aligned} B &= \frac{PM}{2} = \frac{30\cdot 8}{2} = 120 \\ b &= \frac{pm}{2} = \frac{18\cdot 5}{2} = 45 \\ A_\ell &= \frac{(P+p)m’}{2} = \frac{(30+18)\cdot 10}{2} = \frac{48\cdot 10}{2} = 240 \\ A_t &= A_\ell + B + b \\ &= 240 + 120 + 45 \\ &= 405\ \text{cm}^{2} \end{aligned}\]

Nota: ajuste as alternativas para incluir \(405\ \text{cm}^{2}\) (ou use \(m’=8\) para obter \(A_t=365\ \text{cm}^{2}\), opção B).

Conclusão

Para o tronco de pirâmide regular, memorize: \(V=\dfrac{h}{3}(B+\sqrt{Bb}+b)\), \(A_\ell=\dfrac{(P+p)m’}{2}\), \(A_t=A_\ell+B+b\) e \( {m’}^{2}=h^{2}+(M-m)^{2}\). Essas fórmulas são recorrentes no ENEM e em vestibulares.

TRONCO DE PIRÂMIDE – Geometria Espacial

TRONCO DE PIRÂMIDE – Geometria Espacial

O que é o tronco de pirâmide?

📘 Fórmulas do Tronco de Pirâmide Regular

Exemplo 1 (dados P, p, M, m e h)

📗 eBook de Fórmulas Matemáticas

Exemplos Adicionais

Exercícios de Múltipla Escolha

Conclusão

Fórmula Área do Cilindro

CILINDRO – Geometria Espacial

Esfera

"Artigo escrito por"

Adriano Rocha

Nos ajude compartilhando esse post 😉

👉🟢+ de 90 Mapas Mentais de Matemática

Veja também...

Cilindro — Volume, Área Lateral e Área Total

Paralelepípedo e Cubo — Volume e Área Tota

Prismas: Volume e Área Total

Geometria Espacial: Tabela Completa de Fórmulas dos Sólidos

TRONCO DE PIRÂMIDE – Geometria Espacial

TRONCO DE CONE – Geometria Espacial

📘 Baixe Grátis o eBook de Fórmulas Matemática

📘 Mapas Mentais

📚 10 E-books de Matemática

Questões

Conteúdo

Banca