UNICAMP 2020 – Geometria: Área de Triângulo
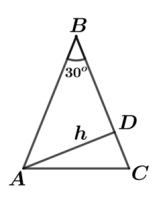
A figura abaixo exibe o triângulo \( ABC \), em que \( AB = BC \) e \( AD \) é uma altura de comprimento \( h \).
A área do triângulo \( ABC \) é igual a:
a) \( h^2 \)
b) \( \sqrt{2}\,h^2 \)
c) \( \sqrt{3}\,h^2 \)
d) \( 2h^2 \)
- Identificação do triângulo:
Seja \( \ell = AB = BC \) e \( S \) a área do triângulo \( ABC \). - Usando o triângulo AHB (ângulo de 30°): \[ \sin 30^\circ = \frac{h}{\ell} = \frac{1}{2} \quad \Rightarrow \quad \ell = 2h \]
- Área do triângulo: \[ S = \frac{BC \cdot h}{2} = \frac{2h \cdot h}{2} = h^2 \]
Resposta correta: a) \( h^2 \)
