UNICAMP 2021 – Questão sobre Triângulos
Considere que os ângulos internos de um triângulo formam uma progressão aritmética.
Dado que \( a, b, c \) são as medidas dos lados do triângulo, com \( a < b < c \),
é correto afirmar que:
a) \( b^2 + ac = a^2 + c^2 \)
b) \( a^2 + bc = b^2 + c^2 \)
c) \( a^2 – bc = b^2 + c^2 \)
d) \( b^2 – ac = a^2 + c^2 \)
a) \( b^2 + ac = a^2 + c^2 \)
b) \( a^2 + bc = b^2 + c^2 \)
c) \( a^2 – bc = b^2 + c^2 \)
d) \( b^2 – ac = a^2 + c^2 \)
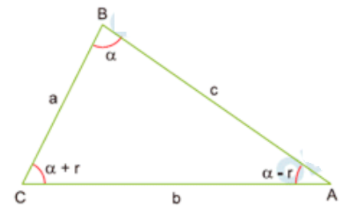
- Seja \( \alpha \) o ângulo médio do triângulo e \( r \) a razão da progressão aritmética dos ângulos.
Então: \[ A = \alpha – r, \quad B = \alpha, \quad C = \alpha + r \] - A soma dos ângulos internos é: \[ (\alpha-r)+\alpha+(\alpha+r)=3\alpha=180^\circ \Rightarrow \alpha=60^\circ \]
- Aplicando a Lei dos Cossenos no triângulo \( ABC \): \[ b^2 = a^2 + c^2 – 2ac \cdot \cos 60^\circ \] \[ b^2 = a^2 + c^2 – ac \] \[ b^2 + ac = a^2 + c^2 \]
- Portanto, a alternativa correta é a **A**.
📘 Questões MATEMÁTICA UNICAMP Resolvidas
Escolha o ano e acesse as questões com solução passo a passo: