UNICAMP 2021 – Questão de Trigonometria
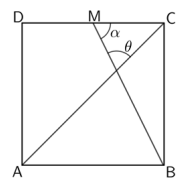
A figura abaixo exibe um quadrado \(ABCD\) em que \(M\) é o ponto médio do lado \(CD\).
Com base na figura, \( \tan(\theta) + \tan(\alpha) \) é igual a:
a) 7 b) 6 c) 5 d) 4
Com base na figura, \( \tan(\theta) + \tan(\alpha) \) é igual a:
a) 7 b) 6 c) 5 d) 4
- Seja \( \ell \) a medida do lado do quadrado.
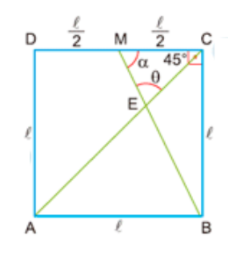
- No triângulo \( BCM \): \[ \tan(\alpha) = \frac{\ell}{\ell/2} = 2 \]
- No triângulo \( CEM \): \[ 45^\circ + \theta + \alpha = 180^\circ \Rightarrow \theta + \alpha = 135^\circ \] \[ \tan(\theta + \alpha) = \tan 135^\circ = -1 \]
- Usando a fórmula da tangente da soma: \[ \frac{\tan\theta + \tan\alpha}{1 – \tan\theta \tan\alpha} = -1 \] Substituindo \(\tan\alpha = 2\): \[ \frac{\tan\theta + 2}{1 – 2\tan\theta} = -1 \]
- Resolvendo: \[ \tan\theta + 2 = -1 + 2\tan\theta \] \[ \tan\theta = 3 \]
- Portanto: \[ \tan\theta + \tan\alpha = 3 + 2 = 5 \] **Resposta: C**
📘 Questões MATEMÁTICA UNICAMP Resolvidas
Escolha o ano e acesse as questões com solução passo a passo:

























