Márcia está decorando sua casa para o Natal e pretende cobrir uma pilastra com papel de parede de temas natalinos e depois enrolar uma fita de lâmpadas de led na pilastra coberta, dando uma única volta, de modo que o ponto em que a fita começa a ser enrolada esteja exatamente embaixo do ponto onde ela termina, como ilustrado na figura a seguir.
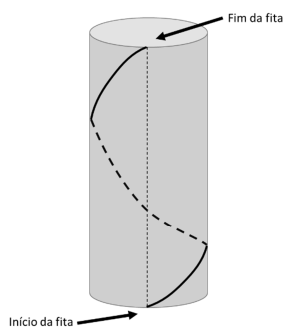
A pilastra tem o formato de um cilindro circular reto com 3 m de altura; a medida do perímetro da circunferência da base é 1 m, e sua lateral será coberta completamente com papel de parede colado sem sobreposição.
a) Sabendo que o metro quadrado do papel de parede custa R$ 20,00,
determine quanto Márcia terá que gastar em papel de parede para cobrir a pilastra.
b) Qual é o menor comprimento que a fita de led precisa ter para ser possível essa instalação?
a) Cálculo do custo com papel de parede:
A área lateral do cilindro é dada por: \[ A = \text{perímetro da base} \times \text{altura} = 1 \times 3 = 3 \text{ m}^2 \]
O custo total será: \[ 3 \times R\$20,00 = R\$60,00 \]
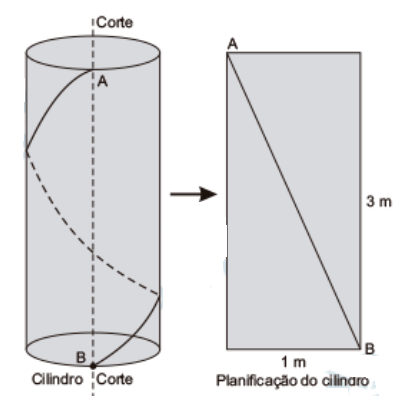
b) Comprimento mínimo da fita de led:
Ao planificar o cilindro, obtemos um retângulo de 3 m de altura e 1 m de base. A fita de led corresponde à diagonal desse retângulo: \[ d = \sqrt{1^2 + 3^2} = \sqrt{10}\text{ m} \]
Resposta final:
- a) R$ 60,00
- b) \(\sqrt{10}\) m
📘 Questões MATEMÁTICA UNICAMP Resolvidas
Escolha o ano e acesse as questões com solução passo a passo: