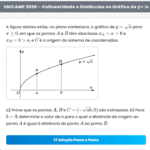
O gráfico de uma parábola de equação \( y = ax^2 + bx + c \) passa pelos pontos \( P=(0,-4) \), \( Q=(2,-1) \) e \( M=(-2,5) \). O valor do produto \( a \cdot b \cdot c \) é:
a) 6 b) 7 c) 8 d) 9
1º Passo – Substituir o ponto \( P=(0,-4) \):
\[ -4 = a\cdot0^2 + b\cdot0 + c \implies c=-4 \]
2º Passo – Montar o sistema com os outros pontos:
Para \( Q=(2,-1) \): \[ -1 = 4a + 2b – 4 \implies 4a+2b=3 \] Para \( M=(-2,5) \): \[ 5 = 4a -2b -4 \implies 4a-2b=9 \]
3º Passo – Resolver o sistema:
Somando as equações: \[ 8a = 12 \implies a = \frac{3}{2} \] Substituindo em \( 4a + 2b = 3 \): \[ 6 + 2b = 3 \implies b = -\frac{3}{2} \]
4º Passo – Calcular \( a \cdot b \cdot c \):
\[ a \cdot b \cdot c = \frac{3}{2} \cdot \left(-\frac{3}{2}\right) \cdot (-4) = 9 \]
Resposta Final: **Alternativa D**
📘 Questões MATEMÁTICA UNICAMP Resolvidas
Escolha o ano e acesse as questões com solução passo a passo: