Ana está treinando as habilidades matemáticas de seu irmão mais novo. Ela escolheu dois números reais \( x \) e \( y \) e avisou para seu irmão que esses números satisfazem as desigualdades: \[ |x-2|\le 2 \quad \text{e} \quad |y-3|\le 1 \] O que o irmão de Ana pode concluir corretamente sobre esses números?
a) \( x^2 + y^2 \le 9 \) b) \( x + y \ge 10 \) c) \( x + y \le 8 \) d) \( x^2 + y^2 \ge 36 \)
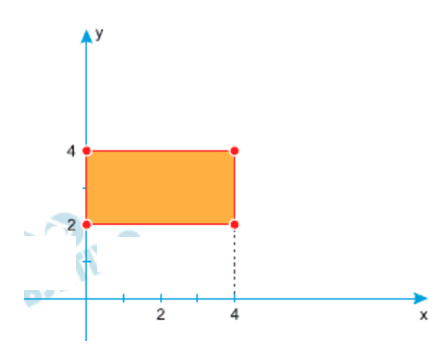
1º Passo – Transformando as desigualdades em intervalos:
\[ |x-2| \le 2 \implies 0 \le x \le 4 \] \[ |y-3| \le 1 \implies 2 \le y \le 4 \]
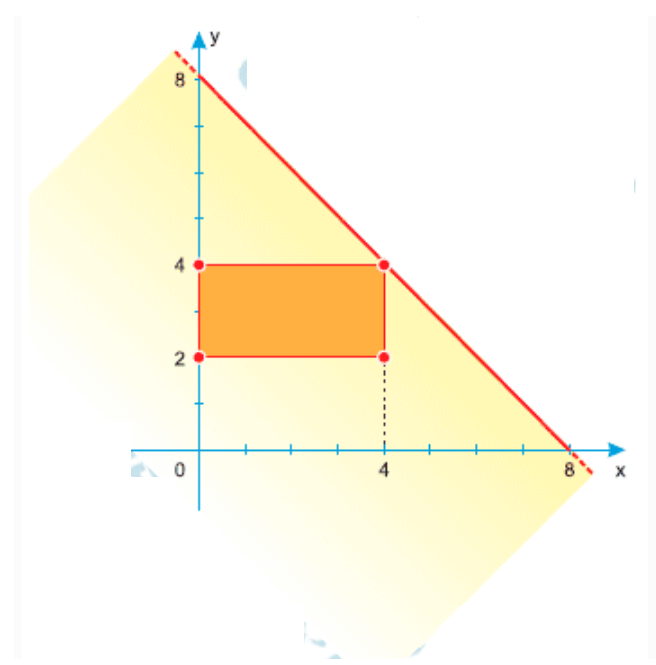
2º Passo – Região de interseção com x+y ≤ 8:
A inequação \( x+y \le 8 \) representa a região abaixo da reta que passa pelos pontos (8,0) e (0,8). Observando o retângulo formado pelos intervalos de \(x\) e \(y\), ele está totalmente contido nesta região.
3º Passo – Conclusão:
Logo, o irmão de Ana pode concluir que: \[ x+y \le 8 \]
Resposta Final: **Alternativa C**
📘 Questões MATEMÁTICA UNICAMP Resolvidas
Escolha o ano e acesse as questões com solução passo a passo: