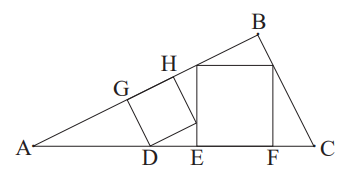
A figura a seguir mostra um triângulo \( ABC \) que contém dois quadrados em seu interior. O segmento \( GH \) é lado de um dos quadrados e está contido em \( AB \). O segmento \( EF \), contido em \( AC \), é lado do outro quadrado. Sabendo que \( AG = 4 \, \text{cm} \) e que o lado \( GH \) do quadrado menor mede \( 3 \, \text{cm} \), o comprimento do segmento \( EF \) é:
a) \( \frac{121}{20} \) b) \( \frac{111}{20} \) c) \( \frac{102}{15} \) d) \( \frac{98}{15} \)
1º Passo – Calcular \( AD \) no triângulo \( AGD \):
Pelo Teorema de Pitágoras: \[ AD^2 = 3^2 + 4^2 = 9 + 16 = 25 \] \[ AD = 5 \text{ cm} \]
2º Passo – Semelhança de triângulos:
Os ângulos \( \angle GAD \), \( \angle EDJ \) e \( \angle HIJ \) são congruentes, logo, os triângulos \( GAD \), \( EDJ \) e \( HIJ \) são semelhantes.
3º Passo – Cálculo de \( EJ \) pela semelhança:
\[ \frac{3}{EJ} = \frac{5}{9} \implies EJ = \frac{27}{5} \]
4º Passo – Cálculo de \( JI \) pela semelhança:
\[ \frac{4}{3} = \frac{JI}{5} \implies JI = \frac{15}{4} \]
5º Passo – Cálculo de \( EF = EI + EJ + JI \):
\[ EF = \frac{9}{5} + \frac{15}{4} + \frac{36+75}{20} = \frac{111}{20} \text{ cm} \]
Resposta Final: \[ \frac{111}{20} \quad \text{(Alternativa B)} \]
