Zero de uma Função

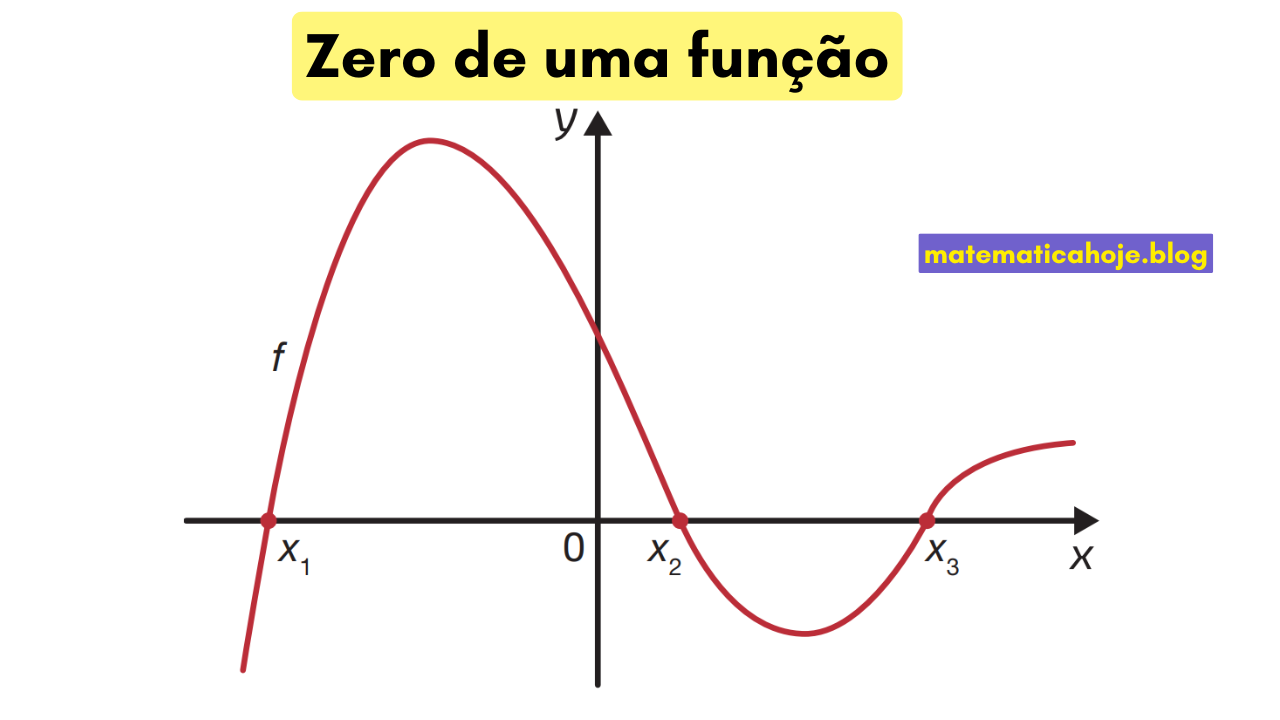
O zero (ou raiz) de uma função \(f\) é qualquer valor \(x\) do domínio para o qual \(f(x)=0\). No gráfico, os zeros são os pontos onde a curva cruza (ou toca) o eixo \(x\). Antes de prosseguir, relembre Plano Cartesiano, Gráfico de uma Função e Domínio. Para treinar, use o Banco de Questões.

Gráfico com três zeros x1, x2 e x3 onde f intercepta o eixo x

Definição. \(x_0\) é zero de \(f\) quando \(f(x_0)=0\). No gráfico, são as abscissas dos pontos de interseção com o eixo \(x\). No gráfico acima, x₁, x₂ e x₃ são raízes.

Como encontrar zeros

1) Pelo gráfico

Leia as abscissas onde a curva encontra o eixo \(x\).
Cruzar o eixo indica zero de multiplicidade ímpar (ex.: simples). Tocar e voltar indica multiplicidade par.

2) Pela equação

Função afim \(f(x)=mx+b\): zero em \(-\dfrac{b}{m}\) (se \(m\neq0\)).
Quadrática \(ax^2+bx+c=0\): use Bhaskara \(\displaystyle x=\frac{-b\pm\sqrt{\Delta}}{2a}\), \(\Delta=b^2-4ac\).
Polinômios: faça fatoração (Fator Comum, Ruffini) e zere cada fator.
Módulo \(|g(x)|=0\): resolve-se \(g(x)=0\).
Racional \(\dfrac{N(x)}{D(x)}\): zeros vêm de \(N(x)=0\) com a restrição \(D(x)\neq0\).
Exponencial \(a^x=k\): \(\,x=\log_a k\). Para zero de \(a^x\) não existe, pois \(a^x>0\).
Log \(\log_a x=0\): \(x=1\).

Exemplos rápidos

Função	Cálculo	Zeros
\(f(x)=2x-6\)	\(2x-6=0\Rightarrow x=3\)	\(3\)
\(g(x)=x^2-5x+6\)	\((x-2)(x-3)=0\)	\(2\) e \(3\)
\(h(x)=x^3-4x\)	\(x(x-2)(x+2)=0\)	\(-2,0,2\)
\(p(x)=(x-1)^2(x+3)\)	Fatores \((x-1)^2\) e \((x+3)\)	\(x=1\) (duplo), \(x=-3\)
\(q(x)=\dfrac{x-2}{x+1}\)	Numerador \(=0\), com \(x\neq-1\)	\(x=2\)
\(r(x)=\|x-4\|\)	\(\|x-4\|=0\Rightarrow x-4=0\)	\(4\)

📘 Apoio para provas: consulte o eBook Fórmulas Matemática (Bhaskara, fatoração, propriedades de módulo e log).

Armadilhas comuns

Domínio: se o \(x\) não pertence ao domínio, não pode ser zero (ex.: \(\sqrt{x-1}\) não tem zero em \(x<1\)).
Racional: se o zero anula numerador e denominador (fator comum), há um buraco; não é zero da função simplificada original.
Exponenciais: \(a^x\) nunca zera (para \(a>0\) e \(a\neq1\)).
Multiplicidade: zero par “toca” o eixo; zero ímpar “cruza”.

➡️ Praticar zeros de funções no Banco de Questões