Enunciado:
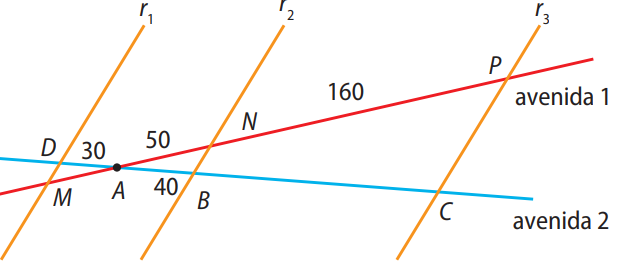
Duas avenidas se encontram em um ponto \( A \). Essas avenidas intersectam três ruas, \( r_1, r_2 \) e \( r_3 \), que são paralelas entre si. Os segmentos de reta \( \overline{AD}, \overline{AB} \) e \( \overline{BC} \) representam quarteirões da avenida 2.
Na figura, estão indicados os comprimentos, em metros, de alguns quarteirões. Determine os comprimentos dos quarteirões representados pelos segmentos de reta \( \overline{BC} \) e \( \overline{AM} \).
👇 Ver solução passo a passo
Passo 1: Aplicando o Teorema de Tales nas retas paralelas \( r_1, r_2, r_3 \), com os segmentos sobre a avenida 1:
\( \frac{AD}{AB} = \frac{MP}{BC} \)
Como:
- \( AD = 30\,m \)
- \( AB = 30 + 50 = 80\,m \)
- \( MP = 160\,m \)
Substituindo na proporção:
\( \frac{30}{80} = \frac{160}{BC} \Rightarrow BC = \frac{160 \cdot 80}{30} = \frac{12800}{30} = \boxed{128\,m} \)
Passo 2: Agora, aplicando a mesma proporção para encontrar \( AM \):
\( \frac{AM}{AD} = \frac{MP}{AB} \Rightarrow \frac{AM}{30} = \frac{160}{80} = 2 \Rightarrow AM = 2 \cdot 15 = \boxed{37{,}5\,m} \)
Resposta final:
- \( \overline{BC} = 128\,m \)
- \( \overline{AM} = 37{,}5\,m \)
🔗 Material complementar gratuito
📌 Quer praticar mais?
Confira uma seleção incrível com 8 exercícios resolvidos sobre Teorema de Tales e Proporcionalidade, todos com figuras, explicações detalhadas e solução passo a passo com botão de abre/fecha:













