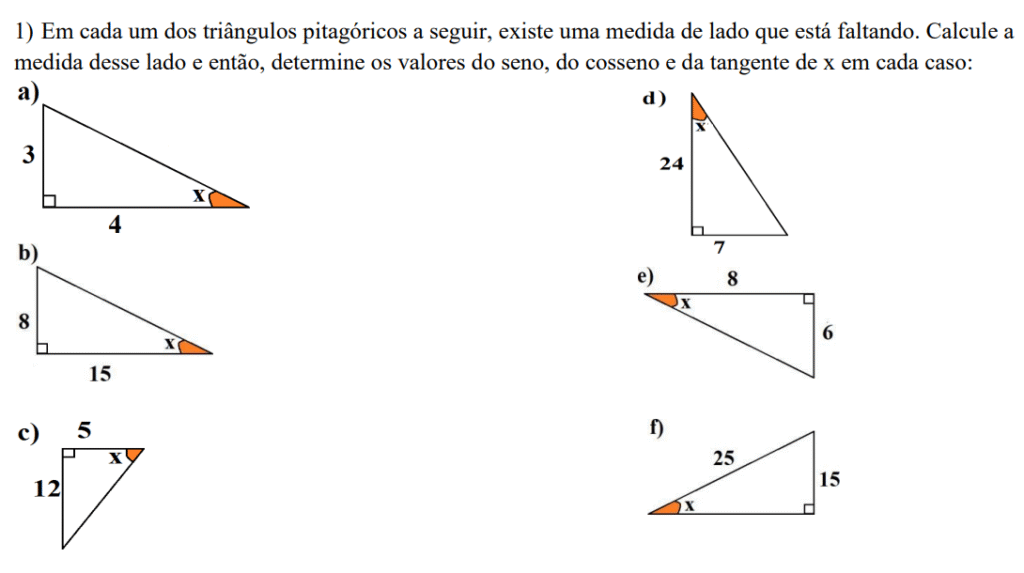
Nos triângulos pitagóricos abaixo, calcule o lado que falta e determine os valores do seno, cosseno e tangente do ângulo \(x\).
\(\sin(x) = \dfrac{\text{cateto oposto}}{\text{hipotenusa}}\) \(\cos(x) = \dfrac{\text{cateto adjacente}}{\text{hipotenusa}}\) \(\tan(x) = \dfrac{\text{cateto oposto}}{\text{cateto adjacente}}\)
📌 Resolução passo a passo
a) 👀Solução passo a passo
Hipotenusa: \( \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \)
\(\sin(x) = \dfrac{3}{5}\), \(\cos(x) = \dfrac{4}{5}\), \(\tan(x) = \dfrac{3}{4}\)
b) 👀Solução passo a passo
Hipotenusa: \( \sqrt{8^2 + 15^2} = \sqrt{64 + 225} = \sqrt{289} = 17 \)
\(\sin(x) = \dfrac{8}{17}\), \(\cos(x) = \dfrac{15}{17}\), \(\tan(x) = \dfrac{8}{15}\)
c) 👀Solução passo a passo
Hipotenusa: \( \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13 \)
\(\sin(x) = \dfrac{5}{13}\), \(\cos(x) = \dfrac{12}{13}\), \(\tan(x) = \dfrac{5}{12}\)
d) 👀Solução passo a passo
Hipotenusa: \( \sqrt{24^2 + 7^2} = \sqrt{576 + 49} = \sqrt{625} = 25 \)
\(\sin(x) = \dfrac{24}{25}\), \(\cos(x) = \dfrac{7}{25}\), \(\tan(x) = \dfrac{24}{7}\)
e) 👀Solução passo a passo
Hipotenusa: \( \sqrt{64 + 36} = \sqrt{100} = 10 \)
\(\sin(x) = \dfrac{4}{5}\), \(\cos(x) = \dfrac{3}{5}\), \(\tan(x) = \dfrac{4}{3}\)
f) 👀Solução passo a passo
Cateto oposto: \( \sqrt{25^2 – 15^2} = \sqrt{625 – 225} = \sqrt{400} = 20 \)
\(\sin(x) = \dfrac{4}{5}\), \(\cos(x) = \dfrac{3}{5}\), \(\tan(x) = \dfrac{4}{3}\)
📘 Aprofunde seus estudos com nossos materiais exclusivos:
📚 Coleção de Livros Indispensáveis
Volume 3: Trigonometria
Domine a trigonometria com explicações claras, exemplos práticos e conteúdo completo para estudo.
🔗 Acesse na AmazonVolume 9: Geometria Plana
Estude os conceitos de geometria plana com uma abordagem didática e repleta de exemplos.
🔗 Acesse na AmazonVolume 10: Geometria Espacial
Aprofunde-se nos estudos da geometria espacial com conteúdos explicativos e exercícios práticos.
🔗 Acesse na Amazon












