11. Diagramas Lógicos
Os diagramas lógicos, também conhecidos como Diagramas de Venn, são ferramentas visuais utilizadas para representar relações entre conjuntos, proposições ou categorias. Eles facilitam a resolução de problemas de lógica, principalmente em questões envolvendo relações de inclusão, interseção e diferença.
11.1 Conceito de Conjuntos
Antes de explorar os diagramas lógicos, é importante relembrar os conceitos básicos de conjuntos:
Conjunto: Uma coleção de elementos que compartilham uma propriedade comum. Representado por letras maiúsculas (ex.: A, B, C).
Exemplo: A={1,2,3}
Relações entre conjuntos:
Inclusão (⊂): Um conjunto está totalmente contido em outro.
Exemplo: A={1,2} ⊂ B={1,2,3,4}
Interseção (∩): Elementos comuns entre dois conjuntos.
Exemplo: A={1,2,3}, B={2,3,4}:
A∩B = {2,3}
União (∪): Todos os elementos dos conjuntos, sem repetição.
Exemplo: A={1,2}, B={2,3}:
A∪B = {1,2,3}
Diferença (-): Elementos que pertencem a um conjunto, mas não ao outro.
Exemplo: A={1,2,3}, B={2,3}:
A − B = {1}
👉Curso Gratuito de Raciocínio Lógico para Concursos
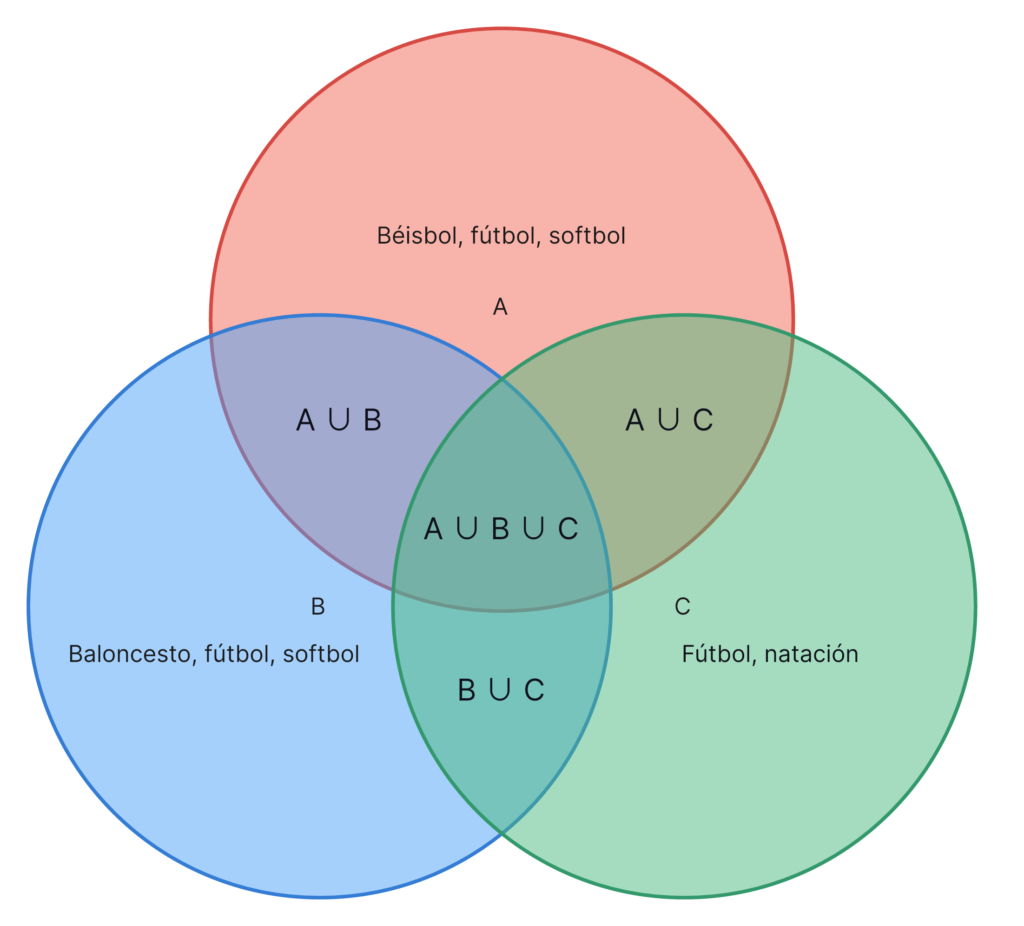
11.2 Diagramas de Venn
Os diagramas de Venn representam os conjuntos graficamente, utilizando círculos para mostrar as relações entre os elementos. São amplamente utilizados em problemas lógicos para:
- Representar categorias.
- Identificar relações de inclusão e interseção.
- Visualizar as diferenças entre conjuntos.
👉Entre no nosso canal do WhatsApp
11.3 Tipos de Problemas com Diagramas Lógicos
- Problemas de Inclusão Total
Representam situações onde um conjunto está contido em outro. Exemplo:
“Todos os gatos são animais.” Diagrama:- Um círculo (gatos) está dentro de outro círculo (animais).
- Problemas de Interseção
Representam situações onde há elementos comuns entre dois ou mais conjuntos. Exemplo:
“Algumas pessoas falam inglês e francês.” Diagrama:- Dois círculos que se interceptam parcialmente representam o grupo de pessoas que falam os dois idiomas.
- Problemas de Diferença
Representam situações em que elementos pertencem a um conjunto, mas não a outro. Exemplo:
“Em uma turma, 30 alunos jogam futebol, 20 jogam vôlei e 10 jogam ambos os esportes. Quantos alunos jogam apenas futebol?” Resolução usando o diagrama:- Total que jogam futebol: 30.
- Interseção (ambos): 10.
- Apenas futebol: 30−10=20
- Problemas com Três Conjuntos
Envolvem relações entre três conjuntos distintos e suas interseções. Exemplo:
“Em uma pesquisa, 40 pessoas gostam de futebol, 30 gostam de basquete e 20 gostam de vôlei. Dessas, 10 gostam de futebol e basquete, 5 gostam de basquete e vôlei, e 8 gostam dos três esportes. Quantas pessoas gostam apenas de futebol?” Resolução:- Representamos os três conjuntos em um diagrama de Venn com interseções.
- Subtraímos os valores das interseções para calcular as áreas que representam “apenas futebol.”
11.4 Como Resolver Questões com Diagramas Lógicos
- Identifique os conjuntos: Liste os grupos mencionados no problema.
- Desenhe os círculos: Cada conjunto será representado por um círculo.
- Preencha as interseções primeiro: Coloque os valores das regiões onde há elementos em comum.
- Preencha as demais áreas: Subtraia os valores das interseções dos totais fornecidos.
- Responda à pergunta: Utilize o diagrama preenchido para encontrar a solução.
11.5 Exemplo Prático
Enunciado:
Em uma turma de 50 alunos:
- 30 estudam matemática.
- 25 estudam física.
- 10 estudam ambas as disciplinas.
Quantos alunos estudam apenas física?
Resolução:
- Desenhe dois círculos representando os conjuntos “matemática” e “física”.
- Preencha a interseção: 10 (ambas as disciplinas).
- Preencha “apenas matemática”: 30−10 = 20
- Preencha “apenas física”: 25−10 = 15
- Total de alunos verificado: 20 (matemática)+15 (física)+10 (ambas) = 45
Resposta: 15 alunos estudam apenas física.
11.6 Exercício Proposto
Em uma pesquisa com 100 pessoas:
- 60 gostam de futebol,
- 50 gostam de basquete,
- 30 gostam de ambos os esportes.
Quantas pessoas gostam apenas de futebol?
Dica: Use o diagrama de Venn para organizar os dados e calcular a resposta.
Conclusão
Os diagramas lógicos são ferramentas essenciais para organizar e resolver problemas envolvendo conjuntos. Eles facilitam a visualização de relações entre elementos, como inclusão, interseção e diferença. A prática constante com questões envolvendo dois ou mais conjuntos é fundamental para dominar esse tipo de problema em concursos públicos.
👉Curso Gratuito de Raciocínio Lógico para Concursos