Domine a função do segundo grau com esta seleção de 10 questões resolvidas passo a passo! Abordamos cálculo de raízes, análise do gráfico, vértice, ponto de máximo e mínimo, interseção com os eixos e muito mais. Ideal para quem estuda para o Enem, vestibulares e concursos. Acesse, visualize as soluções com explicações claras e aproveite os gráficos para entender de vez a parábola!
🧠 Mapas Mentais de MatemáticaQuestão 01. Considere a função definida por:
$$ f(x) = x^2 – 5x + 4 $$
e calcule:
- a) \( f(0) \)
- b) \( f(-4) \)
- c) \( f\left(\dfrac{1}{2}\right) \)
- d) \( f\left(\sqrt{2}\right) \)
🔍 Ver solução passo a passo
a) \( f(0) \)
$$ \begin{align*} f(0) &= 0^2 – 5 \cdot 0 + 4 \\ &= 0 – 0 + 4 \\ &= 4 \end{align*} $$
b) \( f(-4) \)
$$ \begin{align*} f(-4) &= (-4)^2 – 5 \cdot (-4) + 4 \\ &= 16 + 20 + 4 \\ &= 40 \end{align*} $$
c) \( f\left(\frac{1}{2}\right) \)
$$ \begin{align*} f\left(\frac{1}{2}\right) &= \left(\frac{1}{2}\right)^2 – 5 \cdot \frac{1}{2} + 4 \\ &= \frac{1}{4} – \frac{5}{2} + 4 \\ &= \frac{1 – 10 + 16}{4} \\ &= \frac{7}{4} \end{align*} $$
d) \( f\left(\sqrt{2}\right) \)
$$ \begin{align*} f(\sqrt{2}) &= (\sqrt{2})^2 – 5 \cdot \sqrt{2} + 4 \\ &= 2 – 5\sqrt{2} + 4 \\ &= 6 – 5\sqrt{2} \end{align*} $$
✅ Conclusão:
- a) \( f(0) = 4 \)
- b) \( f(-4) = 40 \)
- c) \( f\left(\dfrac{1}{2}\right) = \dfrac{7}{4} \)
- d) \( f\left(\sqrt{2}\right) = 6 – 5\sqrt{2} \)
Questão 02. Um objeto é lançado para cima, a partir do solo, e sua altura \( h \), em metros, varia em função do tempo \( t \), em segundos, de acordo com a expressão:
$$ h(t) = 30t – 5t^2 $$
Qual será a altura do objeto 3 segundos após o lançamento?
- a) 15 metros
- b) 30 metros
- c) 45 metros
- d) 60 metros
- e) 90 metros
🔍 Ver solução passo a passo
Substituindo \( t = 3 \) na função:
$$ \begin{align*} h(3) &= 30 \cdot 3 – 5 \cdot (3)^2 \\ &= 90 – 5 \cdot 9 \\ &= 90 – 45 \\ &= 45 \end{align*} $$✅ Conclusão:
- Altura do objeto após 3 segundos: 45 metros
- Alternativa correta: c)
Questão 03. A soma \( S \) dos \( n \) primeiros números naturais diferentes de zero (1 + 2 + 3 + … + \( n \)) pode ser calculada pela fórmula:
$$ S(n) = \frac{n^2}{2} + \frac{n}{2} $$
Qual é a soma dos 50 primeiros números naturais diferentes de zero?
- a) 1.175
- b) 1.250
- c) 1.275
- d) 1.300
- e) 1.350
🔍 Ver solução passo a passo
Substituindo \( n = 50 \) na fórmula:
$$ \begin{align*} S(50) &= \frac{50^2}{2} + \frac{50}{2} \\ &= \frac{2500}{2} + \frac{50}{2} \\ &= 1250 + 25 \\ &= 1275 \end{align*} $$✅ Conclusão:
- Soma dos 50 primeiros naturais: 1.275
- Alternativa correta: c)
Questão 04. Mensalmente, uma fábrica produz \( x \) unidades de certo produto. Sua produção é vendida por \( (500 – x) \) reais a unidade. Cada unidade tem custo de R$ 100,00. A fábrica ainda possui uma despesa mensal fixa de R$ 10.000,00.
a) Sabendo que o lucro é dado por receita – despesa, determine a função lucro \( L(x) \), em reais:
b) Qual será o lucro quando a fábrica vender 100 produtos?
🔍 Ver solução passo a passo
1) Receita:
Preço de venda por unidade: \( 500 – x \)
Unidades vendidas: \( x \)
$$ R(x) = x \cdot (500 – x) = 500x – x^2 $$
2) Despesa:
Custo por unidade: \( 100x \)
Despesa fixa: \( 10000 \)
$$ D(x) = 100x + 10000 $$
3) Lucro:
$$ L(x) = R(x) – D(x) $$
$$ L(x) = (500x – x^2) – (100x + 10000) $$
$$ L(x) = -x^2 + 400x – 10000 $$
4) Substituindo \( x = 100 \):
$$ L(100) = -(100)^2 + 400 \cdot 100 – 10000 $$
$$ L(100) = -10000 + 40000 – 10000 $$
$$ L(100) = 20000 $$
✅ Conclusão:
- Função lucro: \( L(x) = -x^2 + 400x – 10000 \)
- Lucro para 100 produtos: R$ 20.000,00
Enunciado: Uma função quadrática \( f \) é tal que:
- \( f(0) = 6 \)
- \( f(1) = 2 \)
- \( f(-2) = 20 \)
Determine o valor de \( f\left(\dfrac{1}{2}\right) \).
a) \( \dfrac{7}{4} \)
b) \( \dfrac{11}{4} \)
c) \( \dfrac{15}{4} \)
d) \( \dfrac{19}{4} \)
e) \( \dfrac{23}{4} \)
🔍 Ver solução passo a passo
Seja \( f(x) = ax^2 + bx + c \)
Sabemos que:
1) \( f(0) = c = 6 \)
2) \( f(1) = a(1)^2 + b(1) + c = 2 \)
\( \Rightarrow a + b + 6 = 2 \)
\( \Rightarrow a + b = -4 \) … (I)
3) \( f(-2) = a(-2)^2 + b(-2) + c = 20 \)
\( \Rightarrow 4a – 2b + 6 = 20 \)
\( \Rightarrow 4a – 2b = 14 \) … (II)
Resolvendo o sistema:
Da (I): \( b = -4 – a \)
Substituindo em (II):
\( 4a – 2(-4 – a) = 14 \)
\( 4a + 8 + 2a = 14 \)
\( 6a = 6 \Rightarrow a = 1 \)
\( b = -4 – 1 = -5 \)
Função obtida: \( f(x) = x^2 – 5x + 6 \)
Calculando \( f\left(\dfrac{1}{2}\right) \):
\[ f\left(\dfrac{1}{2}\right) = \left(\dfrac{1}{2}\right)^2 – 5\left(\dfrac{1}{2}\right) + 6 \]
\[ = \dfrac{1}{4} – \dfrac{5}{2} + 6 \]
\[ = \dfrac{1}{4} – \dfrac{10}{4} + \dfrac{24}{4} = \dfrac{15}{4} \]
✅ Resposta correta: letra c) \( \dfrac{15}{4} \)
🧠 Mapas Mentais de MatemáticaQuestão 6. Esboce, no sistema cartesiano, o gráfico de cada função quadrática definida a seguir:
- a) \( y = -x^2 \)
- b) \( y = x^2 – 4 \)
- c) \( y = -x^2 + 6x – 9 \)
- d) \( y = x^2 – 5x \)
Ver solução completa
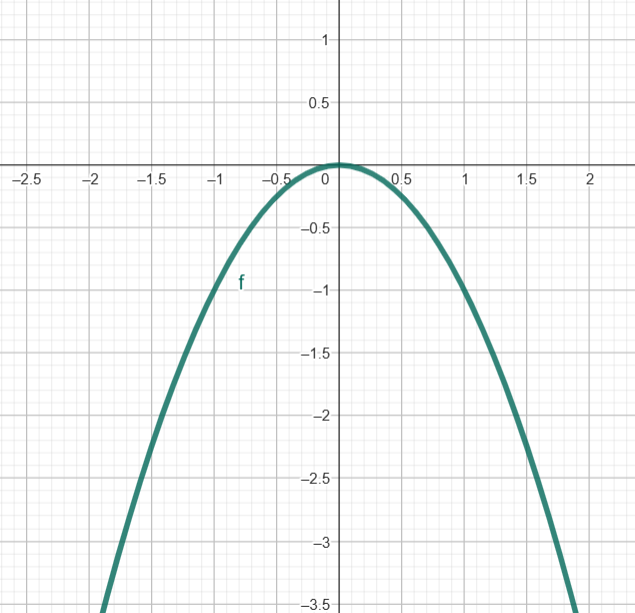
Letra a) \( y = -x^2 \)
Coeficientes: \( a = -1 \), \( b = 0 \), \( c = 0 \)
Vértice: \( x_v = -\frac{b}{2a} = 0 \) ⇒ \( y_v = 0 \)
Raízes: \( y = 0 \Rightarrow -x^2 = 0 \Rightarrow x = 0 \)
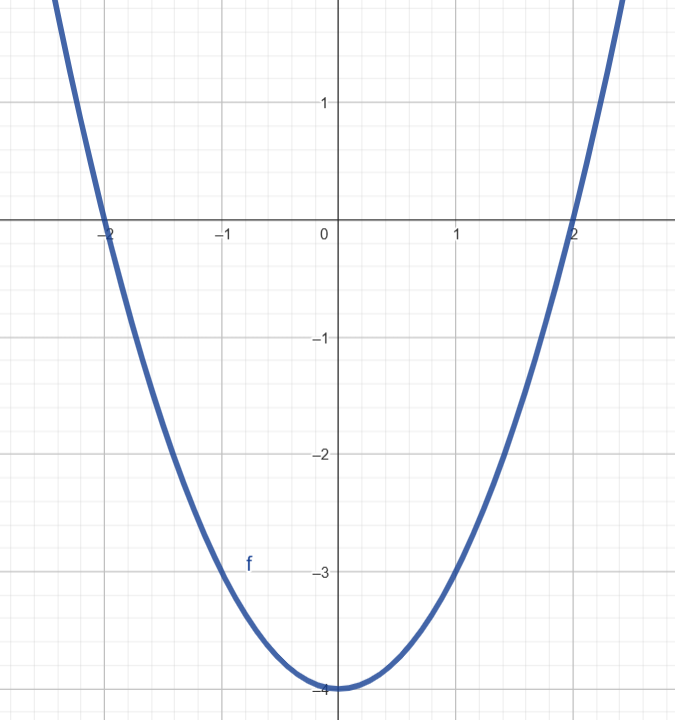
Letra b) \( y = x^2 – 4 \)
Coeficientes: \( a = 1 \), \( b = 0 \), \( c = -4 \)
Vértice: \( x_v = 0 \) ⇒ \( y_v = -4 \)
Raízes: \( x^2 – 4 = 0 \Rightarrow x = \pm 2 \)
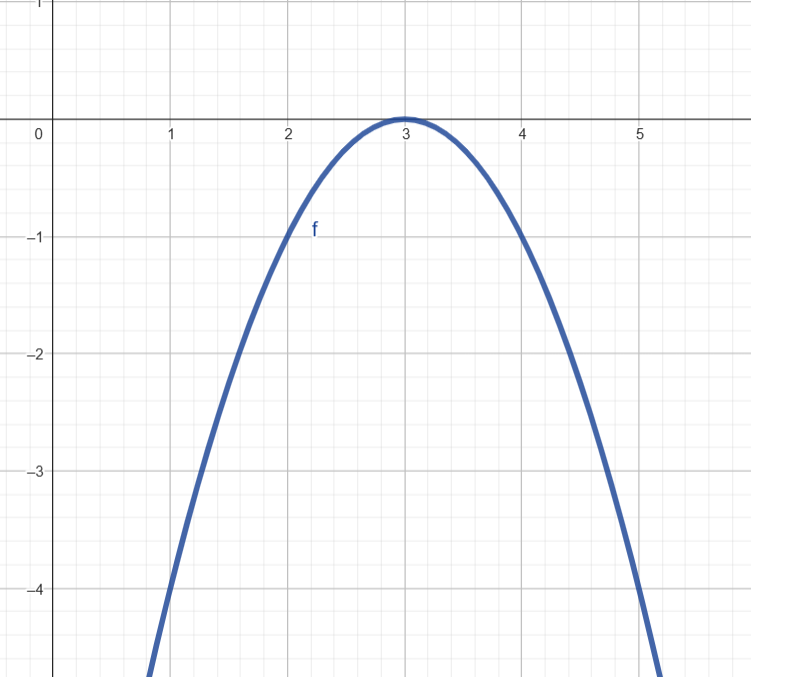
Letra c) \( y = -x^2 + 6x – 9 \)
Coeficientes: \( a = -1 \), \( b = 6 \), \( c = -9 \)
Vértice: \( x_v = -\frac{6}{2 \cdot (-1)} = 3 \)
\( y_v = -3^2 + 6\cdot3 – 9 = -9 + 18 – 9 = 0 \)
Raízes: \( x^2 – 6x + 9 = 0 \Rightarrow (x – 3)^2 = 0 \Rightarrow x = 3 \) (raiz dupla)
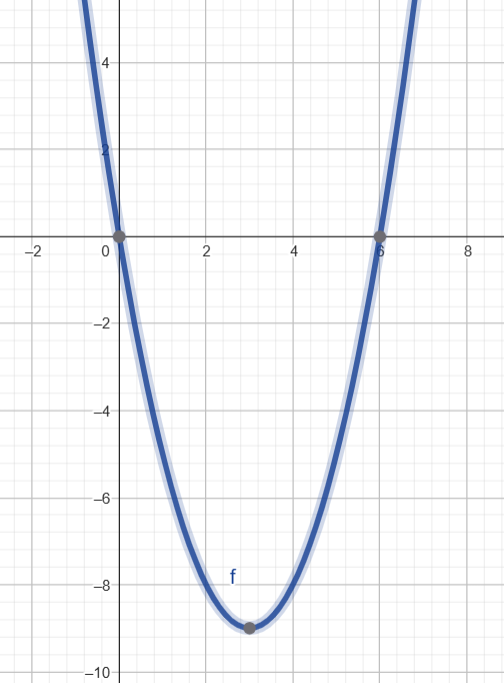
Letra d) \( y = x^2 – 5x \)
Coeficientes: \( a = 1 \), \( b = -5 \), \( c = 0 \)
Vértice: \( x_v = -\frac{-5}{2\cdot1} = \frac{5}{2} \)
\( y_v = \left(\frac{5}{2}\right)^2 – 5\cdot\frac{5}{2} = \frac{25}{4} – \frac{25}{2} = \frac{25 – 50}{4} = \frac{-25}{4} \)
Raízes: \( x(x – 5) = 0 \Rightarrow x = 0 \) ou \( x = 5 \)
Questão 7. Determine o valor de \( m \) para que a parábola que representa a função definida por \( y = 3x^2 – x + m \) passe pelo ponto \( (1, 6) \).
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Queremos que o ponto \( (1, 6) \) pertença ao gráfico da função. Isso significa substituir \( x = 1 \) e \( y = 6 \) na equação e resolver para \( m \).
1) Substituindo na função:
$$ y = 3x^2 – x + m $$
Substituindo \( x = 1 \) e \( y = 6 \):
$$ 6 = 3(1)^2 – 1 + m $$
2) Resolvendo a equação:
$$ 6 = 3 – 1 + m $$
$$ 6 = 2 + m $$
$$ m = 6 – 2 = 4 $$
✅ Conclusão:
- O valor de \( m \) que faz a parábola passar por \( (1, 6) \): $$ \boxed{m = 4} $$
Questão 8. (UEA-AM) A representação gráfica, no plano cartesiano, da função \( f(x) = x^2 – bx + c \), em que \( b \) e \( c \) são números reais, passa pelos pontos \( A(0, 5) \), \( C(5, 0) \) e \( D \).
Sabendo que os pontos \( A \) e \( D \) possuem a mesma ordenada, as coordenadas do ponto \( D \) são:
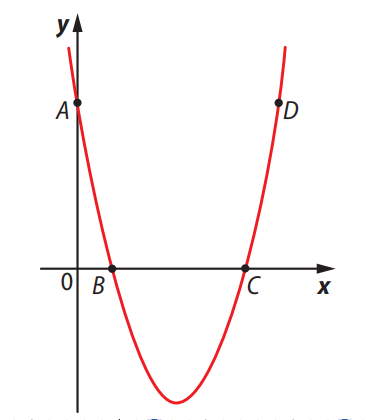
- a) (5, 6)
- b) (6, 0)
- c) (5, 5)
- d) (6, 5)
- e) (6, 6)
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Temos uma parábola que passa pelos pontos \( A(0, 5) \) e \( C(5, 0) \), e queremos saber a coordenada de \( D \), que possui a **mesma ordenada que A**, ou seja, \( y = 5 \).
1) Entendendo a simetria:
Como se trata de uma parábola simétrica, o eixo de simetria passa exatamente no ponto médio entre as raízes.
Sabemos que o ponto \( C(5, 0) \) está na extremidade da parábola (raiz). O outro ponto na base é \( B \), cuja coordenada simétrica em relação a \( x = 2.5 \) seria \( x = 0 \), indicando que a parábola tem simetria horizontal entre os pontos \( A \) e \( D \).
2) Usando simetria para achar \( D \):
O ponto \( A \) está em \( x = 0 \). A raiz da função é em \( x = 5 \), então o eixo de simetria está em:
$$ x_v = \frac{0 + 5}{2} = 2,5 $$
Como \( x = 2,5 \) é o eixo de simetria, o ponto simétrico a \( A(0,5) \) em relação a esse eixo está a 2,5 unidades para a direita de \( x = 2,5 \):
$$ x = 2,5 + 2,5 = 5 $$
Mas o ponto \( C \) já é \( x = 5 \). O simétrico de \( A(0, 5) \) é:
$$ x_D = 2,5 + 2,5 = 5 + 1 = 6 $$
Portanto, como a **mesma ordenada** de \( A \) é 5, temos:
$$ D = (6, 5) $$
✅ Conclusão:
- Coordenadas do ponto \( D \): $$ \boxed{(6,\ 5)} $$












