Questão 9. (UEA-AM) Em um plano cartesiano, a parábola descrita pela função quadrática:
$$ f(x) = x^2 – 4x + 3 $$
tem vértice no ponto \( V \), de abscissa 2, e passa pelo ponto \( P \), de abscissa 4.
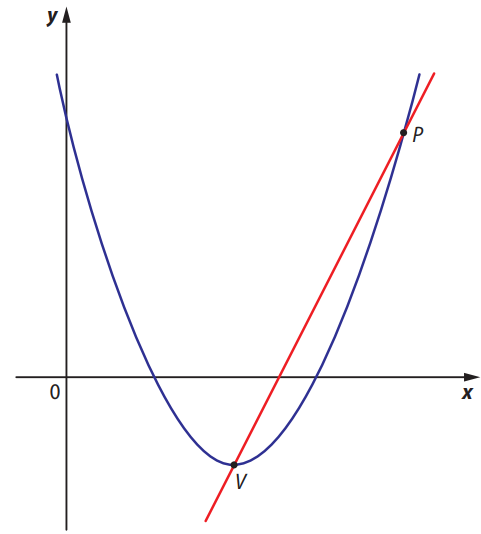
A reta que passa pelos pontos \( P \) e \( V \) intersecta o eixo \( y \) no ponto de ordenada igual a:
a) -2 b) -1 c) -4 d) -3 e) -5
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Devemos encontrar a equação da reta que passa por dois pontos conhecidos da parábola: o vértice \( V = (2, f(2)) \) e o ponto \( P = (4, f(4)) \). Em seguida, determinamos o ponto onde essa reta cruza o eixo \( y \), ou seja, quando \( x = 0 \).
1) Calcular as coordenadas dos pontos:
$$ f(2) = 2^2 – 4 \cdot 2 + 3 = 4 – 8 + 3 = -1 \quad \Rightarrow V(2,\ -1) $$
$$ f(4) = 4^2 – 4 \cdot 4 + 3 = 16 – 16 + 3 = 3 \quad \Rightarrow P(4,\ 3) $$
2) Encontrar a equação da reta \( r \) que passa por \( V \) e \( P \):
Coeficiente angular:
$$ m = \frac{3 – (-1)}{4 – 2} = \frac{4}{2} = 2 $$
Equação da reta na forma reduzida:
$$ y – y_0 = m(x – x_0) $$
$$ y – (-1) = 2(x – 2) $$
$$ y + 1 = 2x – 4 $$
$$ y = 2x – 5 $$
3) Interseção com o eixo \( y \):
Para \( x = 0 \):
$$ y = 2 \cdot 0 – 5 = -5 $$
✅ Conclusão:
- Ordenada do ponto de interseção com o eixo \( y \): $$ \boxed{-5} $$
- Alternativa correta: e)




























