▶️ Estudo do sinal da função quadrática
Aprendemos que estudar o sinal de uma função definida por \( y = f(x) \) significa determinar os valores reais de \( x \in D(f) \) que tornam a função positiva \( f(x) > 0 \), negativa \( f(x) < 0 \) ou nula \( f(x) = 0 \).
O estudo do sinal de uma função quadrática pode ser feito observando o esboço de sua representação gráfica, que, como já estudamos, é uma parábola.
De acordo com a concavidade da parábola, relacionada ao coeficiente a, e com a quantidade de zeros da função, relacionada ao valor de Δ, podemos esboçar o gráfico de uma função quadrática e fazer o estudo do sinal, como veremos a seguir:
• Considerando \( a > 0 \), temos as seguintes possibilidades:
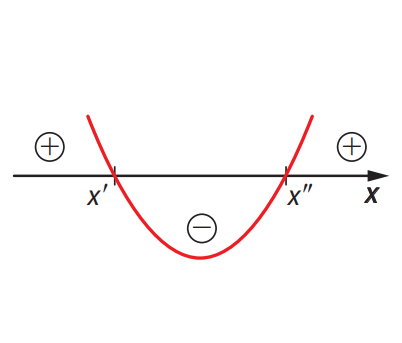 ]
]A função quadrática admite dois zeros reais distintos.
- \( f(x) > 0 \) para \( x < x' \) ou \( x > x” \)
- \( f(x) < 0 \) para \( x' < x < x'' \)
- \( f(x) = 0 \) para \( x = x’ \) ou \( x = x” \)
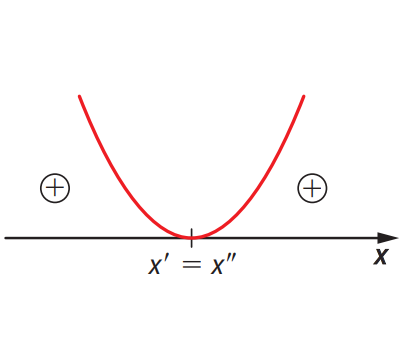 ]
]A função quadrática admite dois zeros reais iguais.
- \( f(x) = 0 \) para \( x = x’ = x” \)
- \( f(x) > 0 \) para \( x \neq x’ \)
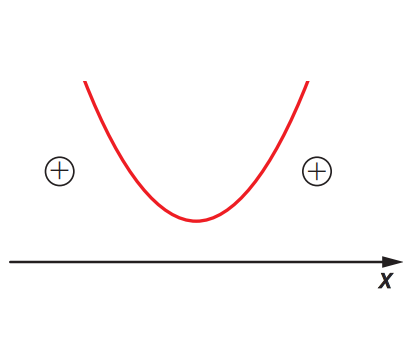 ]
]A função quadrática não admite zeros reais.
- \( f(x) > 0 \) para todo \( x \in \mathbb{R} \)
• Considerando \( a < 0 \), temos as seguintes possibilidades:
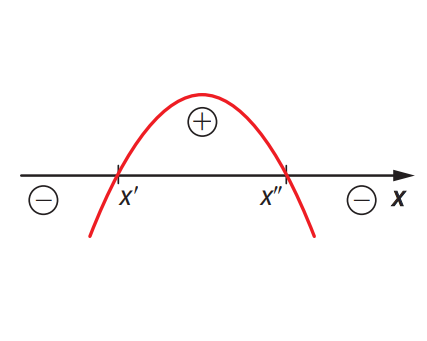 ]
]A função quadrática admite dois zeros reais distintos.
- \( f(x) < 0 \) para \( x' < x < x'' \)
- \( f(x) > 0 \) para \( x < x' \) ou \( x > x” \)
- \( f(x) = 0 \) para \( x = x’ \) ou \( x = x” \)
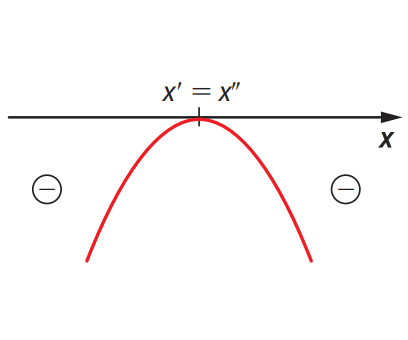 ]
]A função quadrática admite dois zeros reais iguais.
- \( f(x) = 0 \) para \( x = x’ = x” \)
- \( f(x) < 0 \) para \( x \neq x' \)
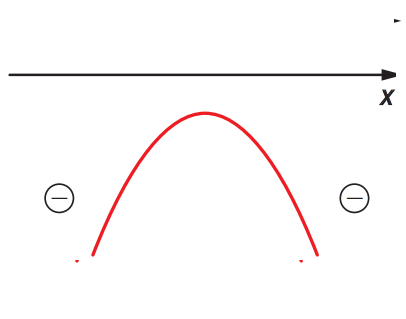 ]
]A função quadrática não admite zeros reais.
- \( f(x) < 0 \) para todo \( x \in \mathbb{R} \)




























