Função Quadrática: 11 Questões Resolvidas Passo a Passo com Gráficos, Sinais, Inequações e Aplicações Práticas

🔎 Entendendo o enunciado:

Queremos determinar em quais intervalos a função é positiva ou negativa.

1) Raízes da equação:

$$ x^2 – 3x – 10 = 0 $$

Utilizando Bhaskara:

$$ \Delta = (-3)^2 – 4 \cdot 1 \cdot (-10) = 9 + 40 = 49 $$

$$ x = \frac{-(-3) \pm \sqrt{49}}{2 \cdot 1} = \frac{3 \pm 7}{2} $$

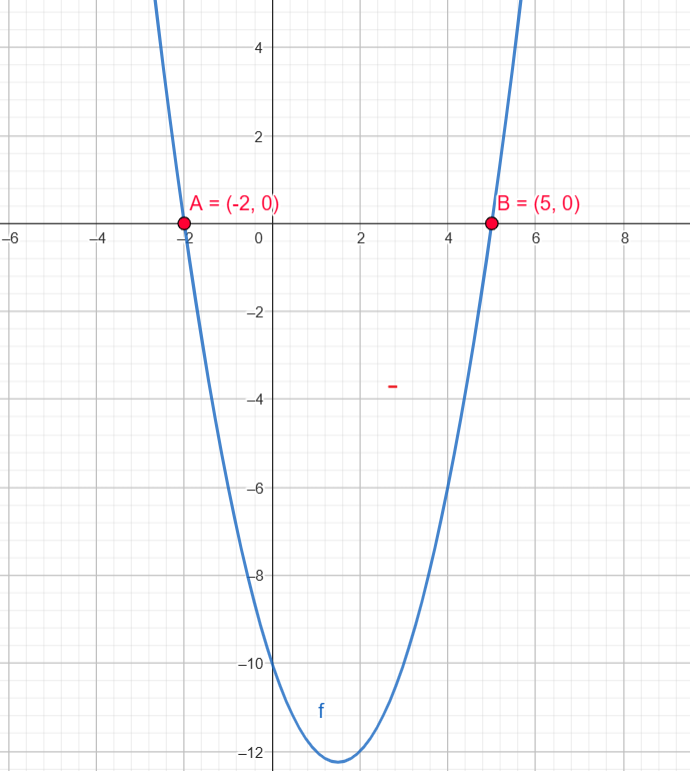
Raízes: \( x_1 = -2 \), \( x_2 = 5 \)

2) Estudo do sinal:

Como o coeficiente de \( x^2 \) é positivo, a parábola é voltada para cima:

• Negativa em \( (-2, 5) \)
• Positiva em \( (-\infty, -2) \cup (5, \infty) \)
• Nula em \( x = -2 \) e \( x = 5 \)

✅ Conclusão:

• f(x) > 0: \( x < -2 \) ou \( x > 5 \)
• f(x) = 0: \( x = -2 \) e \( x = 5 \)
• f(x) < 0: \( -2 < x < 5 \)

1) Raízes:

$$ -x^2 + 2x = 0 \Rightarrow x(-x + 2) = 0 $$

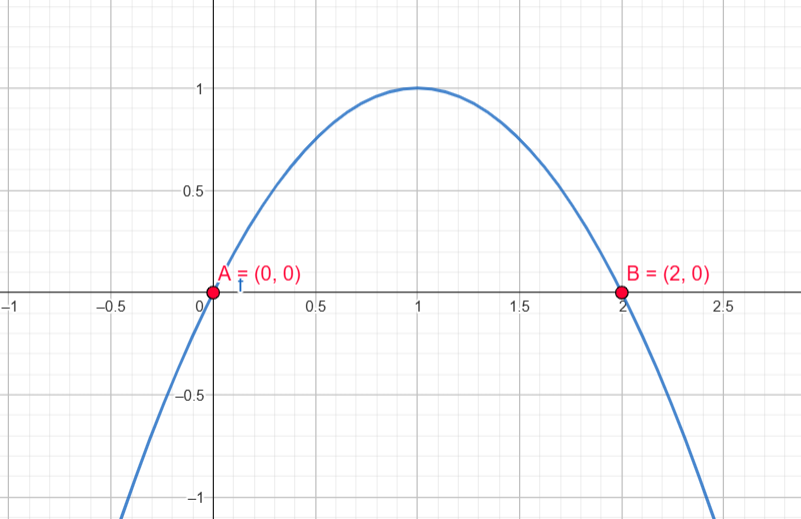
Raízes: \( x = 0 \) e \( x = 2 \)

2) Estudo do sinal:

Coeficiente de \( x^2 \) é negativo: concavidade para baixo

• Positiva entre \( (0, 2) \)
• Negativa fora desse intervalo

✅ Conclusão:

• f(x) > 0: \( 0 < x < 2 \)
• f(x) = 0: \( x = 0 \) e \( x = 2 \)
• f(x) < 0: \( x < 0 \) ou \( x > 2 \)

1) Raízes:

$$ f(x) = -4x^2 + 4x – 1 $$

$$ \Delta = 4^2 – 4 \cdot (-4) \cdot (-1) = 16 – 16 = 0 $$

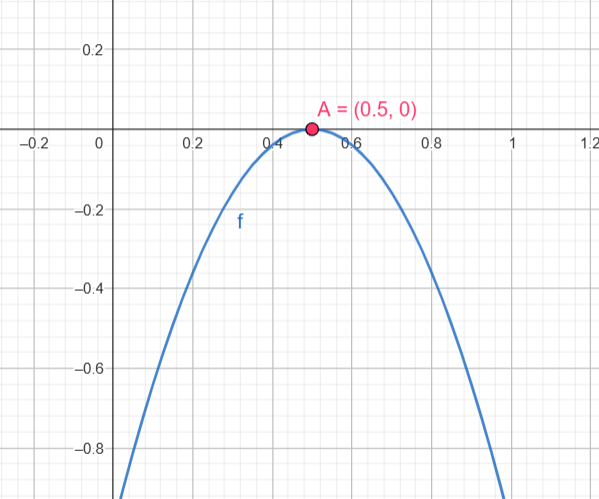
Raiz dupla: \( x = \frac{-4}{2 \cdot -4} = \frac{1}{2} \)

2) Estudo do sinal:

Parábola para baixo e toca o eixo em um único ponto:

• Nunca é positiva
• Apenas nula em \( x = \frac{1}{2} \)
• Negativa em todos os outros valores

✅ Conclusão:

• f(x) = 0: \( x = \frac{1}{2} \)
• f(x) < 0: \( x \neq \frac{1}{2} \)

1) Raízes:

$$ f(x) = x^2 – x + 10 $$

$$ \Delta = (-1)^2 – 4 \cdot 1 \cdot 10 = 1 – 40 = -39 $$

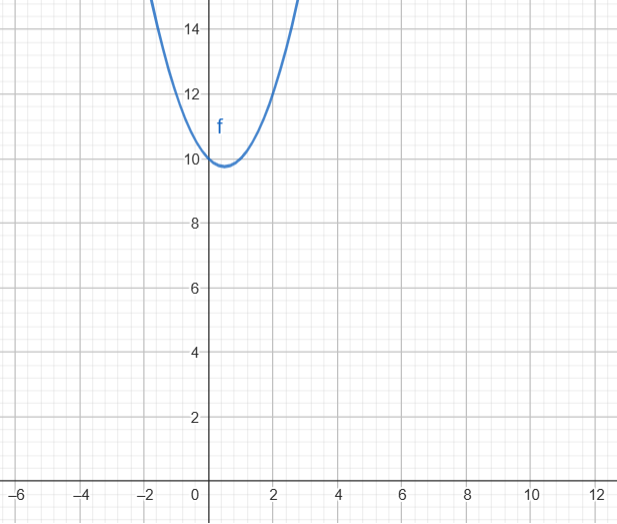
Não possui raízes reais.

2) Estudo do sinal:

Parábola para cima e não corta o eixo x. Portanto, é sempre positiva.

✅ Conclusão:

• f(x) > 0: Para todo \( x \in \mathbb{R} \)

🔎 Entendendo o enunciado:

Queremos encontrar valores de \( m \) para que a função quadrática seja **sempre positiva**, ou seja, **não tenha raízes reais** e o gráfico esteja acima do eixo \( x \).

1) A função é sempre positiva se:

• O coeficiente de \( x^2 \) for positivo (a > 0)
• O discriminante \( \Delta \) for negativo

Como o coeficiente de \( x^2 \) é 1 (positivo), basta garantir:

$$ \Delta = b^2 – 4ac < 0 $$

2) Substituindo os coeficientes:

Na função \( f(x) = x^2 – (2m + 1)x + m^2 \), temos:

\( a = 1,\quad b = -(2m + 1),\quad c = m^2 \)

$$ \Delta = [-(2m+1)]^2 – 4 \cdot 1 \cdot m^2 = (2m+1)^2 – 4m^2 $$

Expandindo:

$$ (2m+1)^2 = 4m^2 + 4m + 1 $$

$$ \Delta = 4m^2 + 4m + 1 – 4m^2 = 4m + 1 $$

3) Impor que \( \Delta < 0 \):

$$ 4m + 1 < 0 \Rightarrow m < -\frac{1}{4} $$

4) Conclusão:

A função será sempre positiva se:

• O valor de \( m \) for menor que \( -\frac{1}{4} \)

Como a condição já foi dada no enunciado (\( m \in \mathbb{R},\ m < -\frac{1}{4} \)), **todos os valores permitidos para \( m \)** satisfazem a condição.

✅ Conclusão:

• Todo \( m < -\frac{1}{4} \) torna \( f(x) > 0 \) para todo \( x \in \mathbb{R} \).

🔎 Entendendo o enunciado:

Queremos determinar os valores de \( k \) que tornam a função sempre negativa, ou seja, a parábola deve estar totalmente abaixo do eixo \( x \).

1) Condições para função sempre negativa:

• Coeficiente de \( x^2 \) negativo → \( a < 0 \)
• Discriminante \( \Delta < 0 \)

2) Identificando os coeficientes:

Na função \( f(x) = kx^2 – 2kx + k – 1 \), temos:

• \( a = k \)
• \( b = -2k \)
• \( c = k – 1 \)

Vamos calcular o discriminante:

$$ \Delta = b^2 – 4ac = (-2k)^2 – 4(k)(k – 1) $$ $$ \Delta = 4k^2 – 4k(k – 1) = 4k^2 – 4k^2 + 4k = 4k $$

3) Impor \( \Delta < 0 \):

$$ 4k < 0 \Rightarrow k < 0 $$

Essa já é a condição do enunciado. Portanto, **todo \( k < 0 \)** torna \( \Delta < 0 \) e o gráfico sempre negativo.

✅ Conclusão:

• f(x) < 0 para todo \( x \in \mathbb{R} \) se \( \boxed{k < 0} \)

1) Resolver a equação:

$$ x^2 – 2x – 8 = 0 \Rightarrow \Delta = (-2)^2 – 4 \cdot 1 \cdot (-8) = 4 + 32 = 36 $$

$$ x = \frac{2 \pm \sqrt{36}}{2} = \frac{2 \pm 6}{2} \Rightarrow x_1 = -2,\ x_2 = 4 $$

2) Estudo do sinal:

Coeficiente de \( x^2 \) é positivo, então a parábola é voltada para cima.

• \( f(x) < 0 \) entre as raízes

✅ Conclusão:

• Solução: \( x \in (-2, 4) \)

1) Resolver a equação:

$$ 9x^2 – 8x – 1 = 0 \Rightarrow \Delta = (-8)^2 – 4 \cdot 9 \cdot (-1) = 64 + 36 = 100 $$

$$ x = \frac{8 \pm \sqrt{100}}{18} = \frac{8 \pm 10}{18} \Rightarrow x_1 = -\frac{1}{9},\ x_2 = 1 $$

2) Estudo do sinal:

Parábola voltada para cima.

• \( f(x) \geq 0 \) fora das raízes

✅ Conclusão:

• Solução: \( x \leq -\frac{1}{9} \) ou \( x \geq 1 \)

1) Calcular \( \Delta \):

$$ -3x^2 + 2x – 1 = 0 \Rightarrow \Delta = 2^2 – 4 \cdot (-3) \cdot (-1) = 4 – 12 = -8 $$

2) Como \( \Delta < 0 \), não há raízes reais.

Parábola voltada para baixo ⇒ sempre negativa.

Mas queremos \( f(x) > 0 \) ⇒ nunca ocorre.

✅ Conclusão:

• Solução: Conjunto vazio \( \varnothing \)

1) Resolver a equação:

$$ -x^2 + 4x – 4 = 0 \Rightarrow \Delta = 4^2 – 4 \cdot (-1) \cdot (-4) = 16 – 16 = 0 $$

Raiz dupla: \( x = \frac{-4}{2 \cdot (-1)} = 2 \)

2) Sinal da função:

Parábola para baixo, toca o eixo em \( x = 2 \)

Função negativa para todo \( x \neq 2 \)

✅ Conclusão:

• Solução: \( x \in \mathbb{R} \setminus \{2\} \)

🔎 Etapa 1: Desenvolver os dois lados

Esquerda:

$$ (2x – 5)(x – 4) = 2x^2 – 8x – 5x + 20 = 2x^2 – 13x + 20 $$

$$ (2x – 5)(x – 4) – 7 = 2x^2 – 13x + 13 $$

Direita:

$$ (x – 2)(x – 3) = x^2 – 3x – 2x + 6 = x^2 – 5x + 6 $$

🔎 Etapa 2: Trazer todos os termos para um lado

$$ 2x^2 – 13x + 13 \geq x^2 – 5x + 6 $$

$$ 2x^2 – 13x + 13 – x^2 + 5x – 6 \geq 0 $$

$$ x^2 – 8x + 7 \geq 0 $$

🔎 Etapa 3: Resolver a inequação

$$ x^2 – 8x + 7 = 0 \Rightarrow \Delta = (-8)^2 – 4 \cdot 1 \cdot 7 = 64 – 28 = 36 $$

$$ x = \frac{8 \pm \sqrt{36}}{2} = \frac{8 \pm 6}{2} \Rightarrow x = 1 \text{ ou } x = 7 $$

Como a parábola é voltada para cima, temos:

• \( f(x) \geq 0 \) fora do intervalo entre as raízes

✅ Conclusão:

• Solução: \( x \leq 1 \) ou \( x \geq 7 \)

🔎 Etapa 1: Calcular \( f(1) \)

$$ f(1) = 1^2 – 3 \cdot 1 + 8 = 1 – 3 + 8 = 6 $$

Substituímos na inequação:

$$ f(x) \geq 12 $$

🔎 Etapa 2: Resolver \( f(x) = x^2 – 3x + 8 \geq 12 \)

$$ x^2 – 3x + 8 \geq 12 \Rightarrow x^2 – 3x – 4 \geq 0 $$

🔎 Etapa 3: Resolver a equação associada

$$ x^2 – 3x – 4 = 0 \Rightarrow \Delta = (-3)^2 – 4 \cdot 1 \cdot (-4) = 9 + 16 = 25 $$

$$ x = \frac{3 \pm \sqrt{25}}{2} = \frac{3 \pm 5}{2} \Rightarrow x_1 = -1,\ x_2 = 4 $$

🔎 Etapa 4: Estudo do sinal

Parábola voltada para cima ⇒ \( f(x) \geq 12 \) fora das raízes

• Solução: \( x \leq -1 \) ou \( x \geq 4 \)

✅ Conclusão:

• Solução: \( x \in \mathbb{R} \ | \ x \leq -1 \text{ ou } x \geq 4 \)

1) Resolver a inequação:

$$ h(t) = -5t^2 + 7t + 6 \geq 8 $$ $$ -5t^2 + 7t + 6 – 8 \geq 0 $$ $$ -5t^2 + 7t – 2 \geq 0 $$

2) Resolver a equação associada:

$$ -5t^2 + 7t – 2 = 0 \Rightarrow \Delta = 49 – 4 \cdot (-5) \cdot (-2) = 49 – 40 = 9 $$

$$ t = \frac{-7 \pm \sqrt{9}}{2 \cdot -5} = \frac{-7 \pm 3}{-10} \Rightarrow t_1 = \frac{4}{10} = 0{,}4,\quad t_2 = 1 $$

3) Estudo do sinal:

Parábola para baixo, \( h(t) \geq 8 \) entre as raízes:

$$ \Rightarrow t \in [0{,}4,\ 1] $$

4) Conferir se está dentro do intervalo dado:

O intervalo original é \( \left[\frac{2}{5}, 1\right] = [0{,}4;\ 1] \)

✅ Conclusão:

• Solução: \( t \in [0{,}4;\ 1] \)

1) Identificar a concavidade:

Coeficiente de \( t^2 \) é negativo ⇒ concavidade para baixo.

2) O vértice da parábola é o ponto de máximo:

$$ t_v = \frac{-b}{2a} = \frac{-7}{2 \cdot (-5)} = \frac{7}{10} = 0{,}7 $$

3) Calcular \( h(0{,}7) \):

$$ h(0{,}7) = -5 \cdot (0{,}7)^2 + 7 \cdot 0{,}7 + 6 = -5 \cdot 0{,}49 + 4{,}9 + 6 = -2{,}45 + 10{,}9 = 8{,}45 $$

4) Imagem da função:

Como é concava para baixo, a imagem vai de mínimo até o vértice.

Vamos calcular os extremos do intervalo:

• Valor mínimo ocorre em \( t = \frac{2}{5} = 0{,}4 \):
• $$ h(0{,}4) = -5 \cdot 0{,}16 + 7 \cdot 0{,}4 + 6 = -0{,}8 + 2{,}8 + 6 = 8 $$
• Valor máximo = \( 8{,}45 \)

✅ Conclusão:

• Imagem: \( \text{Im}(h) = (-∞;\ 8{,}45] \)

1) Identificar os coeficientes:

$$ a = -1,\quad b = 30,\quad c = -5 $$

2) O lucro máximo ocorre no vértice da parábola:

$$ x_v = \frac{-b}{2a} = \frac{-30}{2 \cdot (-1)} = 15 $$

3) Substituir na função para encontrar o lucro máximo:

$$ L(15) = -(15)^2 + 30 \cdot 15 – 5 = -225 + 450 – 5 = 220 $$

✅ Conclusão:

• Lucro máximo: R$ 220,00
• Ocorrendo em: \( x = 15 \) unidades vendidas

1) Queremos que \( L(x) \geq 195 \)

$$ -x^2 + 30x – 5 \geq 195 $$ $$ -x^2 + 30x – 200 \geq 0 $$

2) Resolver a equação associada:

$$ -x^2 + 30x – 200 = 0 \Rightarrow \Delta = 30^2 – 4 \cdot (-1) \cdot (-200) = 900 – 800 = 100 $$

$$ x = \frac{-30 \pm \sqrt{100}}{2 \cdot (-1)} = \frac{-30 \pm 10}{-2} \Rightarrow x = 10 \text{ ou } x = 20 $$

3) Estudo do sinal da parábola:

Como \( a = -1 \), a parábola é voltada para baixo.

• \( L(x) \geq 195 \) entre as raízes.

✅ Conclusão:

• Solução: \( x \in [10,\ 20] \)

1) Calcular a função lucro:

$$ L(n) = [-5n^2 + 100n – 320] – [5 + 10n] $$ $$ L(n) = -5n^2 + 90n – 325 $$

2) Queremos que \( L(n) > 0 \):

$$ -5n^2 + 90n – 325 > 0 $$

Multiplicamos por -1 (inverte o sinal):

$$ 5n^2 – 90n + 325 < 0 $$

3) Resolver a equação associada:

$$ \Delta = (-90)^2 – 4 \cdot 5 \cdot 325 = 8100 – 6500 = 1600 $$

$$ n = \frac{90 \pm \sqrt{1600}}{2 \cdot 5} = \frac{90 \pm 40}{10} $$ $$ \Rightarrow n_1 = 5,\quad n_2 = 13 $$

4) Como a parábola é voltada para cima, \( L(n) > 0 \) entre as raízes:

$$ n \in (5,\ 13) $$

5) Restringindo ao intervalo \( [4, 16] \):

• Solução final: \( n \in \mathbb{R} \ | \ 5 < n < 13 \)

1) Função do lucro:

$$ L(n) = -5n^2 + 90n – 325 $$

2) Máximo ocorre no vértice:

$$ n_v = \frac{-b}{2a} = \frac{-90}{2 \cdot (-5)} = 9 $$

3) Substituir na função lucro:

$$ L(9) = -5 \cdot 9^2 + 90 \cdot 9 – 325 = -405 + 810 – 325 = 80 $$

✅ Conclusão:

• n = 9 proporciona o maior lucro
• Lucro máximo: R$ 80,00

1) Calcular a função lucro:

$$ L(n) = [-5n^2 + 100n – 320] – [5 + 10n] $$ $$ L(n) = -5n^2 + 90n – 325 $$

2) Queremos que \( L(n) > 0 \):

$$ -5n^2 + 90n – 325 > 0 $$

Multiplicamos por -1 (inverte o sinal):

$$ 5n^2 – 90n + 325 < 0 $$

3) Resolver a equação associada:

$$ \Delta = (-90)^2 – 4 \cdot 5 \cdot 325 = 8100 – 6500 = 1600 $$

$$ n = \frac{90 \pm \sqrt{1600}}{2 \cdot 5} = \frac{90 \pm 40}{10} $$ $$ \Rightarrow n_1 = 5,\quad n_2 = 13 $$

4) Como a parábola é voltada para cima, \( L(n) > 0 \) entre as raízes:

$$ n \in (5,\ 13) $$

5) Restringindo ao intervalo \( [4, 16] \):

• Solução final: \( n \in \mathbb{R} \ | \ 5 < n < 13 \)

1) Função do lucro:

$$ L(n) = -5n^2 + 90n – 325 $$

2) Máximo ocorre no vértice:

$$ n_v = \frac{-b}{2a} = \frac{-90}{2 \cdot (-5)} = 9 $$

3) Substituir na função lucro:

$$ L(9) = -5 \cdot 9^2 + 90 \cdot 9 – 325 = -405 + 810 – 325 = 80 $$

✅ Conclusão:

• n = 9 proporciona o maior lucro
• Lucro máximo: R$ 80,00

1) Identificar a função do lucro:

$$ L(n) = -200n^2 + 1600n – 2400 $$

2) Verificar a afirmação III:

O máximo ocorre no vértice: $$ n_v = \frac{-b}{2a} = \frac{-1600}{2 \cdot (-200)} = \frac{1600}{400} = 4 $$

Se cada caixa tem 300 picolés: $$ 300 \cdot 4 = 1200 \text{ picolés} $$

Afirmação III está incorreta. O lucro é máximo com 4 caixas = 1200 picolés, e não 1500.

3) Verificar a afirmação I:

Vamos resolver \( L(n) > 0 \):

$$ -200n^2 + 1600n – 2400 > 0 \Rightarrow 200n^2 – 1600n + 2400 < 0 $$

$$ \Delta = 1600^2 – 4 \cdot 200 \cdot 2400 = 2560000 – 1920000 = 640000 $$

$$ n = \frac{1600 \pm \sqrt{640000}}{2 \cdot 200} = \frac{1600 \pm 800}{400} \Rightarrow n_1 = 2,\quad n_2 = 6 $$

Lucro positivo entre as raízes:

$$ n \in (2,\ 6) $$

Afirmação I está correta.

4) Verificar a afirmação II:

Lucro máximo em \( n = 4 \):

$$ L(4) = -200 \cdot 16 + 1600 \cdot 4 – 2400 = -3200 + 6400 – 2400 = 800 $$

Afirmação II está correta: lucro máximo é R$ 800,00.

✅ Conclusão:

• I e II estão corretas.
• Alternativa correta: b) I e II