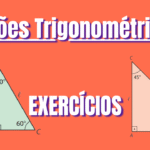
(UFV-MG) Um passageiro em um avião avista duas cidades, \( A \) e \( B \), sob ângulos de \( 15^\circ \) e \( 30^\circ \), respectivamente, conforme a figura a seguir.
Se o avião está a uma altitude de \( 3 \, \text{km} \), a distância entre as cidades \( A \) e \( B \) é:

a) 7 km.
b) 5,5 km.
c) 5 km.
d) 6,5 km.
e) 6 km.
Observando o esquema, nota-se que os ângulos \( \widehat{A \hat{D} B} \) e \( \widehat{D \hat{A} B} \) medem \( 15^\circ \). Assim, o triângulo \( DAB \) é isósceles, e a distância entre as cidades \( A \) e \( B \) é igual a \( BD \).
Para encontrar \( BD \), temos:
Portanto, a distância entre as cidades \( A \) e \( B \) é 6 km (alternativa e).
📖 Leia Também
Descubra tudo sobre ângulos de 30°, 45° e 60° e aprenda as principais razões trigonométricas de forma simples e objetiva.
📚 Coleção de Livros Indispensáveis
Volume 3: Trigonometria
Domine a trigonometria com explicações claras, exemplos práticos e conteúdo completo para estudo.
🔗 Acesse na AmazonVolume 9: Geometria Plana
Estude os conceitos de geometria plana com uma abordagem didática e repleta de exemplos.
🔗 Acesse na AmazonVolume 10: Geometria Espacial
Aprofunde-se nos estudos da geometria espacial com conteúdos explicativos e exercícios práticos.
🔗 Acesse na Amazon