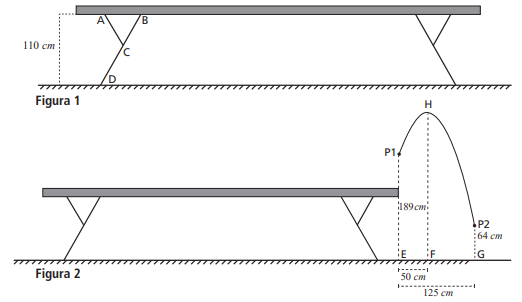
A trave de equilíbrio é um aparelho de ginástica artística. A Figura 1 representa a trave, e a Figura 2 representa um salto da atleta, cuja trajetória do centro de massa é uma parábola.
a) Sabendo que a distância da trave ao solo é 110 cm, calcule o comprimento do segmento \( DB \).
b) A distância horizontal entre a saída e o ponto de aterrissagem é 125 cm, e o ponto mais alto da trajetória é atingido a 50 cm da trave. Sabendo que, ao sair da trave, o centro de massa estava a 189 cm do chão e, no momento da aterrissagem, a 64 cm do chão, determine a **maior altura atingida** pelo centro de massa da atleta.
<
a) Cálculo do segmento \( DB \):
No triângulo retângulo \( BDH \): \[ \sin 60^\circ = \frac{BH}{BD} = \frac{\sqrt{3}}{2} \] Sabendo que \( BH = 110 \, \text{cm} \): \[ \frac{\sqrt{3}}{2} = \frac{110}{BD} \implies BD = \frac{220\sqrt{3}}{3} \, \text{cm} \]
b) Determinação da altura máxima:
A parábola que modela a trajetória tem raízes em \( x=-75 \) e \( x=75 \), em cm: \[ f(x) = a(x-75)(x+75) = a(x^2-75^2) \] Usando o ponto \( P_1(-50,125) \): \[ 125 = a((-50)^2-75^2) = a(2500-5625) = -3125a \] \[ a = -\frac{1}{25} \]
A altura máxima ocorre em \( x=0 \): \[ f(0) = -\frac{1}{25}(-75\cdot 75) = 225 \] Somando a altura do solo ao centro de massa inicial (64 cm): \[ H_\text{máx} = 225 + 64 = 289 \, \text{cm} \]
Resposta Final: a) \( \frac{220\sqrt{3}}{3} \, \text{cm} \) b) \( 289 \, \text{cm} \)
📘 Questões MATEMÁTICA UNICAMP Resolvidas
Escolha o ano e acesse as questões com solução passo a passo:
Adriano Rocha
Nos ajude compartilhando esse post 😉
Veja também...

Ordem das operações na matemática: resolvendo uma expressão com potência e raiz
Expressão numérica com potência e raiz: resolução passo a passo Expressão numérica • Potenciação •

Expressão numérica com potência: resolução passo a passo
Expressão numérica com potência: resolução passo a passo Expressão numérica • Potenciação • Ordem das

Expressão com potenciação: resolvendo passo a passo
Expressão com potenciação: resolução passo a passo Potenciação • Propriedades das potências • Expressões numéricas

Domínio e imagem de uma função no gráfico: resolução passo a passo
Domínio e imagem de uma função no gráfico: resolução passo a passo Funções • Gráfico

Porcentagem de fração aplicada ao tempo: resolvendo passo a passo
Quanto vale 20% de 2/3 de 5 anos? Porcentagem • Frações • Conversão de tempo

Como simplificar uma fração com raízes de forma rápida
Expressão com raiz quadrada: resolução passo a passo Radiciação • Simplificação • Expressão algébrica Expressão

Como resolver expressão com raiz e fração de forma rápida
Valor da expressão com raiz para x = 400: resolução passo a passo Expressão numérica

Porcentagem no gráfico: clientes que avaliaram como Bom ou Ótimo
Porcentagem no gráfico: clientes que avaliaram como Bom ou Ótimo Estatística • Porcentagem • Interpretação

Módulo: o que é, como calcular e como resolver exercícios
Módulo: o que é, como resolver e exercícios básicos e avançados Matemática Hoje • Módulo

Equação com valor absoluto (módulo) resolvida
Equação com valor absoluto Equação com Valor Absoluto Resolva a equação: |x − 3| =

Expressão numérica com potência que faz muita gente errar
Potência e multiplicação juntas: cuidado com a ordem das operações 📘 Quer revisar esse tema

Como resolver |3 − 10| + |2 − 5| – exercício com módulo resolvido
Expressão com valor absoluto Expressão com Valor Absoluto Calcule: |3 − 10| + |2 −

