Triângulo de Pascal — Guia completo com propriedades, aplicações e exercícios
Fluxo vertical otimizado para mobile. Exercícios com enunciado seguido de solução em toggle (azul fechado → verde aberto).
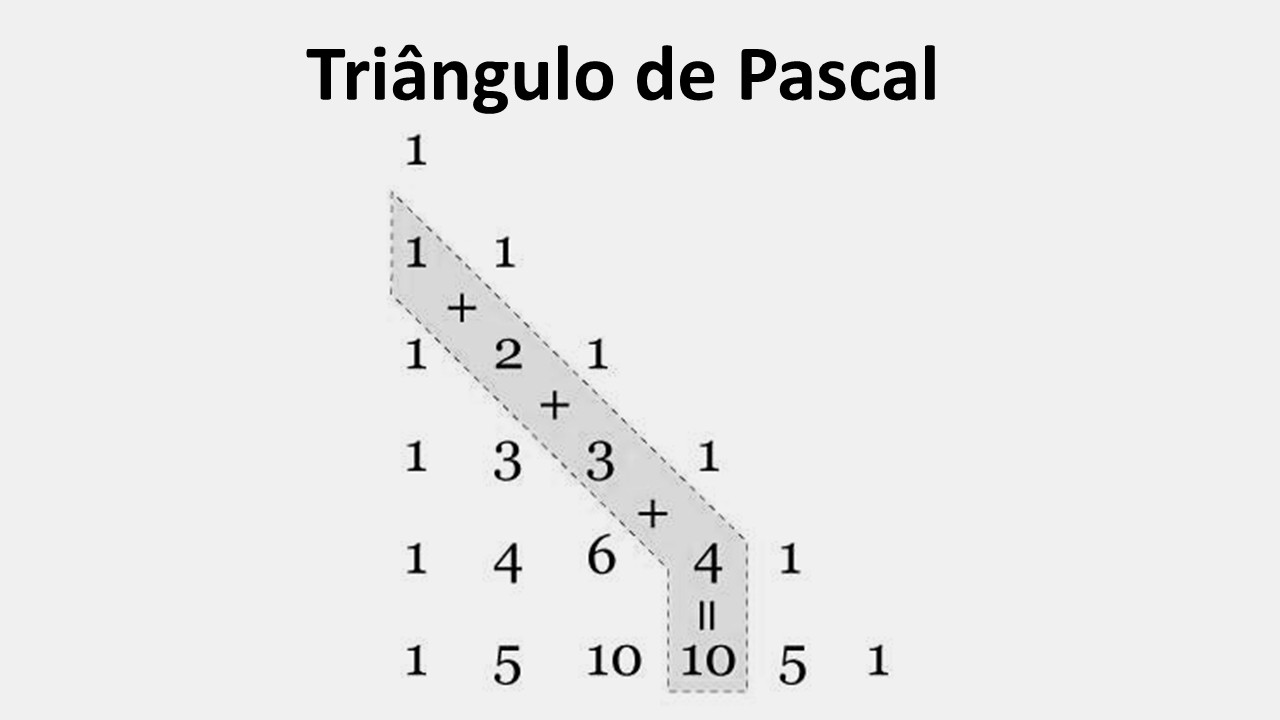
O que é o Triângulo de Pascal e como construir
O Triângulo de Pascal é uma disposição triangular de números inteiros em que cada elemento interno é a soma dos dois números imediatamente acima. A primeira e a última entradas de cada linha são sempre \(1\).
Passo a passo
- Comece pela linha \(0\): 1.
- Cada nova linha começa e termina com 1.
- Para os elementos internos, some os dois “vizinhos” superiores: \(a_{n,k}=a_{n-1,k-1}+a_{n-1,k}\) (com \(1\le k\le n-1\)).
Notação e ligação com combinações
O número na linha \(n\) e coluna \(k\) (contando de \(0\)) é o coeficiente binomial:
\[ a_{n,k}=\binom{n}{k}=\frac{n!}{k!\,(n-k)!},\quad 0\le k\le n. \]
Logo, o Triângulo de Pascal é uma “tabela” de \(\binom{n}{k}\), isto é, das combinações de \(n\) elementos tomados \(k\) a \(k\).
Para reforço: Casos especiais na Análise Combinatória, Fórmulas da Análise Combinatória e Permutação simples.
Propriedades essenciais (com provas curtas)
1) Recorrência de Pascal
\[ \binom{n}{k}=\binom{n-1}{k-1}+\binom{n-1}{k},\qquad 1\le k\le n-1,\ n\ge 1. \]
Interpretação: fixe um elemento “especial”. Ou ele entra no grupo (restam \(k-1\) de \(n-1\)) ou fica fora (escolhem-se \(k\) de \(n-1\)).
2) Simetria
\[ \binom{n}{k}=\binom{n}{n-k},\qquad 0\le k\le n. \]
Escolher \(k\) é equivalente a escolher os \(n-k\) excluídos.
3) Soma da linha \(n\)
\[ \sum_{k=0}^{n}\binom{n}{k}=2^{n},\qquad n\ge 0. \]
A soma conta todos os subconjuntos de um conjunto de \(n\) elementos.
4) “Hockey-stick” (cajado de hóquei)
\[ \sum_{m=r}^{n}\binom{m}{r}=\binom{n+1}{r+1},\qquad 0\le r\le n. \]
Prova por indução a partir da recorrência de Pascal.
5) Diagonais e sequência de Fibonacci
Somando termos em diagonais oblíquas apropriadas obtém-se Fibonacci (com \(F_0=0,\ F_1=1\)):
\[ F_{n}=\sum_{k=0}^{\left\lfloor (n-1)/2\right\rfloor}\binom{n-k-1}{k},\qquad n\ge 1. \]
Binômio de Newton e coeficientes do Triângulo
\[ (x+y)^n=\sum_{k=0}^{n}\binom{n}{k}x^{\,n-k}y^{\,k},\qquad n\in\mathbb{N}. \]
Exemplo — Enunciado
Expandir \((x+y)^5\) usando a linha \(5\) do Triângulo.
Ver solução
Linha \(5\): \(1,5,10,10,5,1\).
\((x+y)^5=x^5+5x^4y+10x^3y^2+10x^2y^3+5xy^4+y^5.\)
Aprofunde: Permutação circular com repetição.
Aplicações rápidas em contagem e probabilidade
Caminhos em grade: de \((0,0)\) a \((m,n)\) com passos “direita”/“cima”: \(\binom{m+n}{m}\).
Lançamentos de moeda: probabilidade de \(k\) caras em \(n\) lançamentos: \(\binom{n}{k}\,2^{-n}\).
Coeficientes em séries: produtos polinomiais usam diretamente a linha correspondente.
Pequena tabela do Triângulo de Pascal (linhas 0 a 8)
| n | Entradas \(\binom{n}{k}\) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | ||||||||
| 1 | 1 | 1 | |||||||
| 2 | 1 | 2 | 1 | ||||||
| 3 | 1 | 3 | 3 | 1 | |||||
| 4 | 1 | 4 | 6 | 4 | 1 | ||||
| 5 | 1 | 5 | 10 | 10 | 5 | 1 | |||
| 6 | 1 | 6 | 15 | 20 | 15 | 6 | 1 | ||
| 7 | 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | |
| 8 | 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 |
Exercícios resolvidos
Exercício 1 — Enunciado
Calcule \(\displaystyle \binom{10}{3}\) usando a fórmula de combinações.
Ver solução
\(\displaystyle \binom{10}{3}=\frac{10!}{3!\,7!}=\frac{10\cdot9\cdot8}{3\cdot2\cdot1}=120.\)
Exercício 2 — Enunciado
Prove que \(\displaystyle \sum_{k=0}^{n}\binom{n}{k}=2^n\).
Ver solução
De \((1+1)^n=\sum_{k=0}^{n}\binom{n}{k}\), segue \(\sum_{k=0}^n\binom{n}{k}=2^n.\)
Exercício 3 — Enunciado
Mostre pela recorrência que \(\binom{8}{4}=70\).
Ver solução
Linha \(8\): \(1,8,28,56,70,56,28,8,1\). Portanto, \(\binom{8}{4}=70\).
Exercício 4 — Enunciado
Conte os caminhos mínimos de \((0,0)\) a \((3,2)\) movendo apenas “direita” e “cima”.
Ver solução
Total de passos: \(5\). Escolha onde ficam os dois “cima”:
\(\displaystyle \binom{5}{2}=10\) caminhos.
Exercício 5 — Enunciado
Expanda \((2x-y)^4\) pela linha \(4\) do Triângulo.
Ver solução
Linha \(4\): \(1,4,6,4,1\).
\((2x-y)^4=16x^4-32x^3y+24x^2y^2-8xy^3+y^4.\)
Exercício 6 — Enunciado
Mostre a simetria: \(\binom{12}{3}=\binom{12}{9}\).
Ver solução
\(\displaystyle \binom{12}{3}=\frac{12!}{3!\,9!}=\frac{12!}{9!\,3!}=\binom{12}{9}.\)
Exercício 7 — Enunciado
Calcule \(\binom{5}{2}+\binom{6}{2}+\binom{7}{2}+\binom{8}{2}\).
Ver solução
Soma direta: \(10+15+21+28=74\).
Via “hockey-stick” desde \(n=r=2\): \(\sum_{n=2}^{8}\binom{n}{2}=\binom{9}{3}=84\). Subtraindo \(\binom{2}{2}+\binom{3}{2}+\binom{4}{2}=1+3+6=10\), resulta \(84-10=74\).
Exercício 8 — Enunciado
Qual a probabilidade de obter exatamente 3 caras em 7 lançamentos de moeda justa?
Ver solução
\(\displaystyle P=\binom{7}{3}\,2^{-7}=\frac{35}{128}.\)
Exercício-relâmpago — Enunciado
Qual é o coeficiente de \(x^4y^3\) em \((x+y)^7\)?
Ver solução
\(\binom{7}{3}=35\).

























