O que é

Um triângulo mágico é um triângulo (geralmente equilátero) no qual colocamos números em pontos específicos dos lados (vértices e posições intermediárias) de forma que a soma em cada lado seja a mesma constante \(S\).

Ao contrário do quadrado mágico (que soma linhas/colunas/diagonais), aqui só interessam as três arestas do triângulo.

Formatos mais usados

  • 1–6 (6 posições): 3 vértices + 3 pontos médios — cada lado contém 3 números.
  • 1–9 (9 posições): 3 vértices + 6 pontos intermediários — cada lado contém 4 números.

Os vértices pertencem a dois lados (contam “duas vezes” quando somamos lado a lado), enquanto os pontos intermediários pertencem a um lado só.

Como calcular a soma-alvo \(S\) (contagem dupla)

Seja \(C\) a soma dos vértices e \(E\) a soma dos demais pontos. Se a soma em cada lado é \(S\), então a soma “lado a lado” vale \(3S\). Pela contagem de incidências:

\[ 3S = 2C + E. \]

Como \(C+E=T\) (soma total dos números usados), obtemos a fórmula prática:

\[ \boxed{\,S=\dfrac{C+T}{3}\,}. \]

Casos clássicos.

  • 1–6: \(T=1+\cdots+6=21\) ⇒ \(S=\dfrac{C+21}{3}\).
  • 1–9: \(T=45\) ⇒ \(S=\dfrac{C+45}{3}\).

Logo, para um conjunto fixo de números, \(S\) depende da escolha dos vértices (de \(C\)). Além disso, \(C+T\) precisa ser múltiplo de 3.

Estratégias de construção

  1. Escolha os vértices primeiro. Valores maiores nos vértices costumam elevar \(S\).
  2. Calcule \(S\) com a fórmula e chegue “informado” para preencher as arestas.
  3. Complete um lado de cada vez, usando a soma que falta para decidir os pontos intermediários.
  4. Use simetria. Rotacionar/refletir uma solução gera outras equivalentes.
Triângulo mágico 1–6: exemplo com soma 9 em cada lado
Exemplo clássico 1–6 (3 números por lado).

Exemplos resolvidos

Exemplo A — Triângulo mágico 1–6 (3 números por lado)

Objetivo: usar os números 1–6 nas 6 posições (3 vértices + 3 pontos) para que cada lado some o mesmo \(S\).

Ver uma solução com \(S=9\)

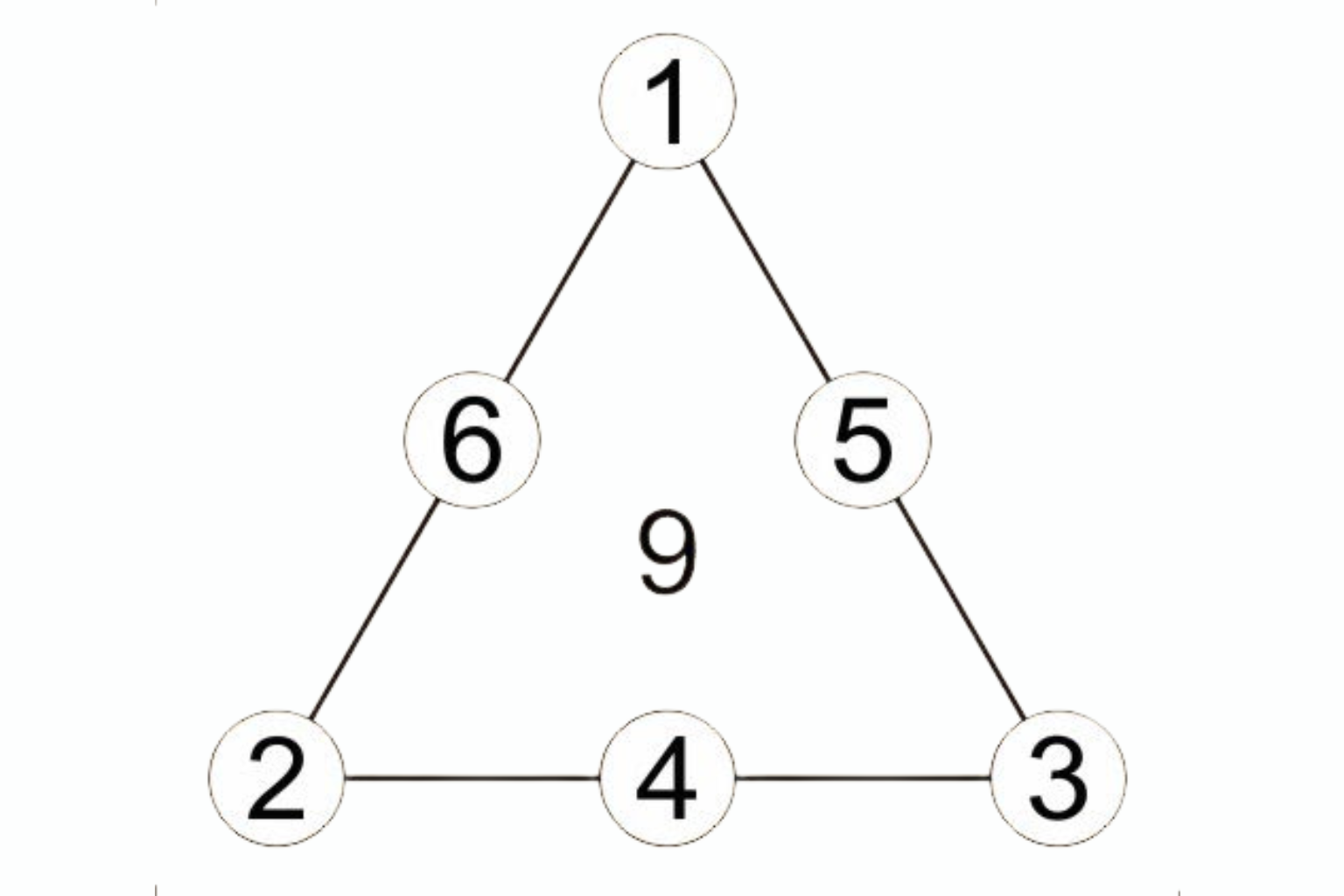
Vértices: \(A=1,\ B=2,\ C=3\) ⇒ \(C=6\). Logo \(S=\dfrac{6+21}{3}=9\).

Pontos nas arestas: AB = 6, BC = 4, CA = 5.

Checagem: AB: \(1+6+2=9\); BC: \(2+4+3=9\); CA: \(3+5+1=9\).

Esta é a configuração exibida na primeira capa do artigo.

Exemplo B — Triângulo mágico 1–9 (4 números por lado)

Objetivo: usar 1–9 nas 9 posições (3 vértices + 6 pontos) para somas iguais.

Ver uma solução com \(S=17\)

Vértices: \(A=1,\ B=2,\ C=3\) ⇒ \(C=6\). Então \(S=\dfrac{6+45}{3}=17\).

Pontos nas arestas: AB = 5 e 9; BC = 4 e 8; CA = 6 e 7.

Checagem: AB: \(1+5+9+2=17\); BC: \(2+4+8+3=17\); CA: \(3+6+7+1=17\).

Generalizações e viabilidade

Qualquer conjunto de números pode ser usado (ex.: 0–5, múltiplos de 5 etc.). A fórmula geral continua valendo: para soma total \(T\) e soma dos vértices \(C\),

\[ S=\frac{C+T}{3}\quad\text{(precisa ser inteiro).} \]

Depois, resta verificar se os números restantes conseguem completar cada lado até \(S\) sem repetições. Em sala de aula, isso vira um excelente problema de backtracking curto.

Para conexões legais: compare o “padrão de vãos e repetições” do triângulo mágico com o Triângulo de Sierpiński (fractal), e contraste com o Triângulo de Penrose (ilusão de perspectiva). A ideia de contagem dupla que usamos aqui conversa com identidades no Triângulo de Pascal.

Exercícios (enunciado + solução em toggle)

Exercício 1 — Enunciado

No caso 1–6, mostre que \(S\) é da forma \(\dfrac{C+21}{3}\). Quais escolhas de vértices tornam \(S\) inteiro?

Ver solução

Da contagem dupla: \(3S=2C+E\) e \(C+E=21\) ⇒ \(3S=C+21\) ⇒ \(S=(C+21)/3\).

Logo, \(C\equiv -21\equiv 0 \ (\mathrm{mod}\ 3)\). As escolhas de vértices devem ter soma múltipla de 3 (ex.: {1,2,3}, {1,5,6}, {2,4,5}, {3,4,6}…).

Exercício 2 — Enunciado

Construa um triângulo mágico 1–6 com \(S=10\) ou explique por que é impossível.

Ver solução

Precisamos de \(S=(C+21)/3=10\) ⇒ \(C=9\). Há várias trincas com soma 9 (ex.: {1,2,6}, {1,3,5}, {2,3,4}). Escolhendo {1,3,5} nos vértices, tente completar as arestas com {2,4,6}. Uma possibilidade é AB=4, BC=6, CA=2, que checa: AB \(1+4+3=8\) (falhou). Ajustando: AB=6, BC=2, CA=4 ⇒ AB \(1+6+3=10\), BC \(3+2+5=10\), CA \(5+4+1=10\). Portanto, é possível.

Exercício 3 — Enunciado

No caso 1–9, prove que \(S=\dfrac{C+45}{3}\) e encontre uma escolha de vértices que torne \(S\) par.

Ver solução

Idêntico ao caso anterior: \(3S=2C+E\) e \(C+E=45\) ⇒ \(S=(C+45)/3\).

Para \(S\) par, \(C+45\) deve ser múltiplo de 6 ⇒ \(C\equiv 3\ (\mathrm{mod}\ 6)\). Ex.: {1,2,6} soma 9 ≡ 3 (mod 6) ⇒ \(S=(9+45)/3=18\) (par). Checa-se por tentativa preenchendo as arestas com os demais números.

Exercício 4 — Enunciado

Generalize: dado um conjunto de números com soma total \(T\), prove que para qualquer triângulo mágico a soma em cada lado é \(S=\dfrac{C+T}{3}\), onde \(C\) é a soma nos vértices.

Ver solução

Cada lado soma \(S\). Somando os três lados dá \(3S\). Ao somar “por pontos”, cada vértice aparece em dois lados (peso 2) e cada ponto intermediário em um lado (peso 1). Logo \(3S=2C+E\). Como \(C+E=T\), segue \(3S=C+T\) ⇒ \(S=(C+T)/3\).