Exercícios sobre a Relação de Euler — \( \boldsymbol{V – E + F = 2} \)
Lista comentada com problemas clássicos e criativos. Soluções em abre/fecha e cálculo vertical. Inclui a extensão topológica \(2-2g\) e armadilhas comuns.
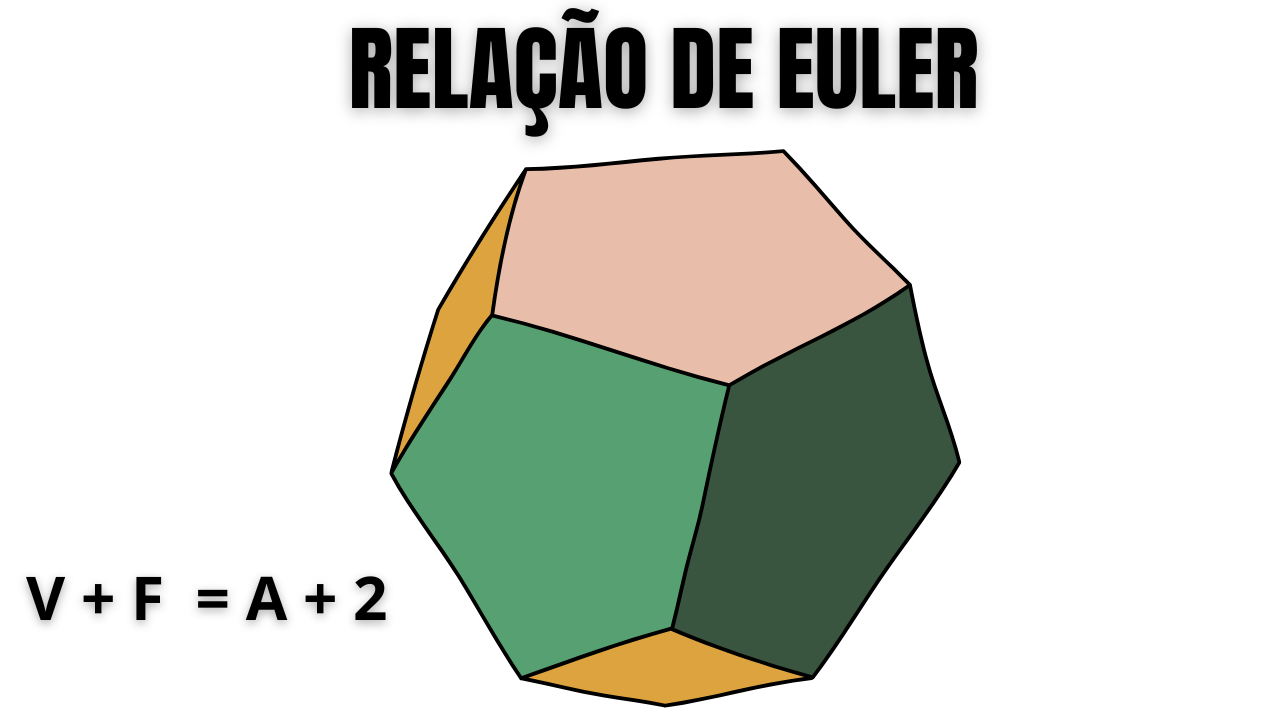
Antes de começar
- Relação de Euler (esfera): \(V – E + F = 2\) — superfície fechada, sem auto-interseção.
- Extensão topológica: \(V – E + F = 2 – 2g\) (gênero \(g\): nº de “furos”, toro \(g=1\)).
- Modelos abertos (com “tampa” faltando) — não aplicam Euler diretamente.
Exercícios discursivos (com solução )
-
1) Um poliedro convexo tem \(F=14\) e \(E=24\). Calcule o número de vértices \(V\).
Ver solução
$$\begin{aligned} V – E + F &= 2\\ V – 24 + 14 &= 2\\ V – 10 &= 2\\ V &= \mathbf{12} \end{aligned}$$ -
2) Um poliedro convexo possui \(V=18\) e \(F=12\). Determine o número de arestas \(E\).
Ver solução
$$\begin{aligned} 18 – E + 12 &= 2\\ 30 – E &= 2\\ E &= 28 \end{aligned}$$Resposta: \(\mathbf{E=28}\).
-
3) Em um poliedro convexo, todas as faces são triangulares. Sabendo que \(E=36\), calcule \(F\) e \(V\).
Ver solução
Malha triangular: \(3F=2E\Rightarrow F=\dfrac{2E}{3}=\dfrac{72}{3}=24\).
$$\begin{aligned} V – 36 + 24 &= 2\\ V – 12 &= 2\\ V &= \mathbf{14} \end{aligned}$$ -
4) Um prisma pentagonal reto tem duas bases pentagonais e cinco faces laterais retangulares. Use Euler para confirmar \(V\), \(E\) e \(F\).
Ver solução
Para prisma de base com \(n=5\): \(V=2n=10\); \(E=3n=15\); \(F=n+2=7\).
$$\begin{aligned} V – E + F &= 10 – 15 + 7\\ &= \mathbf{2}\quad \checkmark \end{aligned}$$ -
5) Uma pirâmide de base hexagonal (convexa) tem \(V, E, F\)? Calcule e verifique Euler.
Ver solução
Base com \(n=6\): vértices da base (6) + ápice (1) ⇒ \(V=7\).
Arestas: 6 da base + 6 ligando ao ápice ⇒ \(E=12\).
Faces: 6 triangulares laterais + 1 base ⇒ \(F=7\).
$$\begin{aligned} V – E + F &= 7 – 12 + 7\\ &= \mathbf{2}\quad \checkmark \end{aligned}$$ -
6) (Topologia) Uma malha poliedral representa um toro (\(g=1\)) com \(V=50\) e \(E=90\). Calcule \(F\).
Ver solução
$$\begin{aligned} V – E + F &= 2 – 2g\\ 50 – 90 + F &= 2 – 2\\ -40 + F &= 0\\ F &= \mathbf{40} \end{aligned}$$ -
7) (Armadilha) Uma “caixa sem tampa” é um prisma retangular aberto (uma face faltando). Ela tem \(V=8\), \(E=12\), \(F=5\). Explique por que Euler não vale.
Ver solução
A superfície não é fechada. Aplicando \(V-E+F\):
$$\begin{aligned} 8 – 12 + 5 &= 1 \ne 2 \end{aligned}$$Sem a face faltante, o sólido não atende a condição — Euler não se aplica diretamente.
-
8) Um poliedro convexo tem \(V=22\) e \(E=36\). Determine \(F\) e diga se a conta é compatível com Euler.
Ver solução
$$\begin{aligned} 22 – 36 + F &= 2\\ -14 + F &= 2\\ F &= \mathbf{16} \end{aligned}$$Compatível: \(22-36+16=2\).
-
9) Um poliedro convexo possui \(F=11\). Se todas as faces são pentagonais, quantas arestas \(E\) e vértices \(V\) ele tem?
Ver solução
Dupla contagem das arestas pelas faces: cada face pentagonal contribui 5 arestas e cada aresta é compartilhada por 2 faces:
$$\begin{aligned} 5F &= 2E \Rightarrow E = \frac{5F}{2} = \frac{55}{2} \end{aligned}$$Não é inteiro ⇒ impossível existir poliedro convexo com todas as 11 faces pentagonais. (Boa armadilha!)
-
10) (Faces quadradas) Um poliedro convexo tem apenas faces quadradas e \(V=12\). Encontre \(E\) e \(F\).
Ver solução
Dupla contagem: \(4F=2E \Rightarrow E=2F\).
$$\begin{aligned} V – E + F &= 2\\ 12 – (2F) + F &= 2\\ 12 – F &= 2\\ F &= 10 \quad\Rightarrow\quad E=2F=20 \end{aligned}$$Resposta: \(F=\mathbf{10}\), \(E=\mathbf{20}\).
-
11) (Triângulos + quadrados) Em um poliedro convexo, há \(F_3\) faces triangulares e \(F_4\) faces quadradas, sem outros tipos. Sabe-se que \(F_3=8\) e \(V=10\). Encontre \(F_4\) e \(E\).
Ver solução
Dupla contagem das arestas pelas faces:
$$\begin{aligned} 3F_3 + 4F_4 &= 2E \quad (1) \end{aligned}$$Euler:
$$\begin{aligned} V – E + (F_3+F_4) &= 2\\ 10 – E + (8+F_4) &= 2\\ 18 – E + F_4 &= 2\\ E &= 16 + F_4 \quad (2) \end{aligned}$$Substitua (2) em (1):
$$\begin{aligned} 3\cdot8 + 4F_4 &= 2(16+F_4)\\ 24 + 4F_4 &= 32 + 2F_4\\ 2F_4 &= 8\\ F_4 &= 4\\ E &= 16 + 4 = \mathbf{20} \end{aligned}$$ -
12) (Gênero \(g=2\)) Uma malha poliedral sobre um duplo toro tem \(F=60\) e \(E=92\). Encontre \(V\).
Ver solução
$$\begin{aligned} V – E + F &= 2 – 2g\\ V – 92 + 60 &= 2 – 4\\ V – 32 &= -2\\ V &= \mathbf{30} \end{aligned}$$ -
13) (Checagem de modelo) Num arquivo 3D de um “cubo” ideal: \(V=8\), \(E=12\), \(F=6\). Verifique Euler. Agora, se apagar uma face, o que acontece?
Ver solução
$$\begin{aligned} 8 – 12 + 6 &= 2 \quad \checkmark\\[4pt] \text{Sem uma face: } 8 – 12 + 5 &= 1 \quad (\text{não é superfície fechada}) \end{aligned}$$ -
14) Em um poliedro convexo, cada vértice é incidente a exatamente 3 faces triangulares. Sabe-se que \(F=20\). Encontre \(V\) e \(E\).
Ver solução
Se todas as faces são triangulares: \(3F=2E \Rightarrow E=\dfrac{3F}{2}=\dfrac{60}{2}=30\).
$$\begin{aligned} V – E + F &= 2\\ V – 30 + 20 &= 2\\ V – 10 &= 2\\ V &= \mathbf{12} \end{aligned}$$ -
15) (Consistência) Um poliedro convexo teria \(V=9\), \(E=15\), \(F=5\). É possível?
Ver solução
$$\begin{aligned} 9 – 15 + 5 &= -1 \ne 2 \end{aligned}$$Inconsistente ⇒ não pode existir como poliedro convexo fechado.
Questões de múltipla escolha (gabarito e Solução)
-
Para poliedros convexos, a Relação de Euler é:
- A) \(V + E + F = 2\)
- B) \(V – E + F = 2\)
- C) \(V – E – F = 2\)
- D) \(V + E – F = 2\)
Gabarito
B -
Uma malha sobre um toro (\(g=1\)) satisfaz \(V – E + F =\)
- A) 2
- B) 1
- C) 0
- D) -2
Gabarito
C (pois \(2-2g=0\)). -
Se todas as faces são quadradas e \(V=14\), então:
- A) \(F=14,\ E=28\)
- B) \(F=12,\ E=24\)
- C) \(F=10,\ E=20\)
- D) \(F=8,\ E=16\)
Gabarito
De \(4F=2E \Rightarrow E=2F\). Euler: \(14 – 2F + F = 2 \Rightarrow 14 – F = 2 \Rightarrow F=12 \Rightarrow E=24\).
Resposta: B.
FAQ — dúvidas rápidas
| Quando posso usar \(V-E+F=2\)? | Em poliedros fechados, sem auto-interseção, com superfície “como a esfera” (gênero 0). |
|---|---|
| E se a figura tiver “furos”? | Use \(V-E+F=2-2g\). Para toro (\(g=1\)), o valor é 0; para duplo toro (\(g=2\)), é -2. |
| Planificações valem para Euler? | Não diretamente: a planificação está “aberta”. Conte \(V,E,F\) na superfície fechada. |