Prisma Regular — guia completo (vertical)
Tudo em sequência: definição → fórmulas → planificação → casos (triangular, quadrangular, pentagonal, hexagonal) → situações-problema → links internos → produtos.
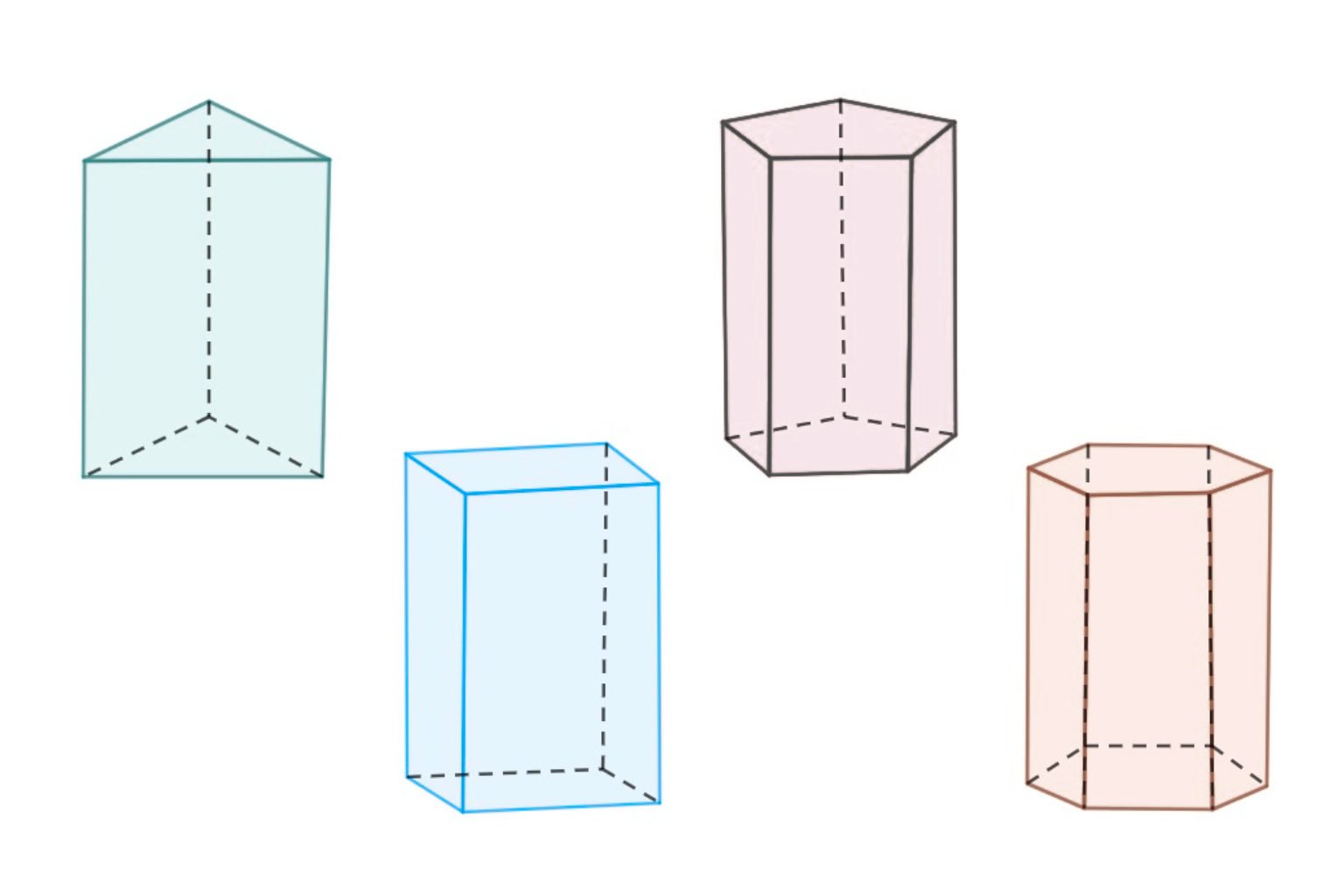
1) O que é um prisma regular?
Prisma regular é o prisma reto cujas bases são polígonos regulares (lados e ângulos iguais). As faces laterais são retângulos e a altura do sólido é a própria aresta lateral \(h\).
Para ver a família completa de sólidos, confira o artigo sobre poliedros e os Sólidos de Platão. A relação entre faces, arestas e vértices é dada pela Fórmula de Euler (e veja exercícios em Relação de Euler – exercícios).
- Perímetro da base: \(p\)
- Apótema da base: \(r\)
- Área da base: \(A_b\)
Para base regular de \(n\) lados (lado \(a\)): \(p=na\) e \(A_b=\dfrac{p\,r}{2}\).
2) Fórmulas essenciais
Quer revisar fórmulas de outros sólidos? Veja: paralelepípedo, volume do paralelepípedo e planificação do paralelepípedo.
3) Planificação do prisma regular
A planificação é composta por um retângulo \(p \times h\) (todas as faces laterais) e duas bases. Disso seguem diretamente \(A_L=p\,h\) e \(A_T=p\,h+2A_b\).
Curtiu planificações? Veja também: planificação do cubo.
4) Prisma triangular regular base: triângulo equilátero
- \(p=3a\)
- \(A_b=\dfrac{\sqrt3}{4}a^2\)
- \(A_L=3a\,h,\quad A_T=3a\,h+\dfrac{\sqrt3}{2}a^2\)
- \(V=\dfrac{\sqrt3}{4}a^2\,h\)
Relembre as propriedades do triângulo equilátero e técnicas gerais em triângulos semelhantes.
Situação-problema (resolvida)
Uma claraboia em forma de prisma triangular regular possui lado da base \(a=10\ \text{cm}\) e altura \(h=12\ \text{cm}\). Calcule a área total e o volume.
$$\begin{aligned} p&=3a=30\\ A_b&=\frac{\sqrt3}{4}\cdot 10^2=25\sqrt3\\ A_L&=p\,h=30\cdot12=360\\[2mm] A_T&=A_L+2A_b=360+2\cdot25\sqrt3=\mathbf{360+50\sqrt3\ \text{cm}^2}\\[2mm] V&=A_b\,h=25\sqrt3\cdot12=\mathbf{300\sqrt3\ \text{cm}^3} \end{aligned}$$5) Prisma quadrangular regular base: quadrado
- \(p=4a\)
- \(A_b=a^2\)
- \(A_L=4a\,h,\quad A_T=4a\,h+2a^2\)
- \(V=a^2\,h\)
Para aprofundar quadriláteros e sólidos aparentados, confira: cubo e paralelepípedo.
Situação-problema (resolvida)
Uma caixa d’água (prisma quadrangular regular) tem \(a=5\ \text{cm}\) e \(h=14\ \text{cm}\) na maquete. Encontre a área total e o volume.
$$\begin{aligned} p&=4a=20\\ A_b&=a^2=25\\ A_L&=p\,h=20\cdot14=280\\[2mm] A_T&=A_L+2A_b=280+2\cdot25=\mathbf{330\ \text{cm}^2}\\[2mm] V&=A_b\,h=25\cdot14=\mathbf{350\ \text{cm}^3} \end{aligned}$$6) Prisma pentagonal regular apótema \(r\)
- \(p=5a\)
- \(A_b=\dfrac{p\,r}{2}=\dfrac{5ar}{2}\)
- \(A_L=5a\,h,\quad A_T=5a\,h+5ar\)
- \(V=\dfrac{5ar}{2}\,h\)
Situação-problema (resolvida)
Um totem é um prisma pentagonal regular com \(a=6\ \text{cm}\), \(r=4{,}13\ \text{cm}\) e \(h=15\ \text{cm}\). Calcule a área lateral e o volume.
$$\begin{aligned} p&=5a=30\\ A_b&=\frac{p\,r}{2}=\frac{30\cdot 4.13}{2}=61.95\\ A_L&=p\,h=30\cdot15=\mathbf{450}\\[2mm] V&=A_b\,h=61.95\cdot15=\mathbf{929.25} \end{aligned}$$7) Prisma hexagonal regular base: hexágono
Para hexágono regular, \(r=\dfrac{\sqrt3}{2}a\).
- \(p=6a\)
- \(A_b=\dfrac{3\sqrt3}{2}a^2\)
- \(A_L=6a\,h,\quad A_T=6a\,h+3\sqrt3\,a^2\)
- \(V=\dfrac{3\sqrt3}{2}a^2\,h\)
Situação-problema (resolvida)
Um reservatório decorativo tem forma de prisma hexagonal regular com \(a=8\ \text{cm}\) e \(h=20\ \text{cm}\). Determine a área total e o volume.
$$\begin{aligned} p&=6a=48\\ r&=\frac{\sqrt3}{2}a=4\sqrt3\\ A_b&=\frac{p\,r}{2}=\frac{48\cdot4\sqrt3}{2}=96\sqrt3\\ A_L&=p\,h=48\cdot20=960\\[2mm] A_T&=A_L+2A_b=960+2\cdot96\sqrt3=\mathbf{960+192\sqrt3\ \text{cm}^2}\\[2mm] V&=A_b\,h=96\sqrt3\cdot20=\mathbf{1920\sqrt3\ \text{cm}^3} \end{aligned}$$8) Dicas rápidas
- Tríade que resolve tudo: \(A_L=p\,h\), \(A_T=A_L+2A_b\), \(V=A_b\,h\).
- Para base regular: \(A_b=\dfrac{p\,r}{2}\) (se souber o apótema \(r\)).
- Planificação: retângulo lateral sempre mede \(p\times h\).





















