Fórmulas do Cone (circular reto)
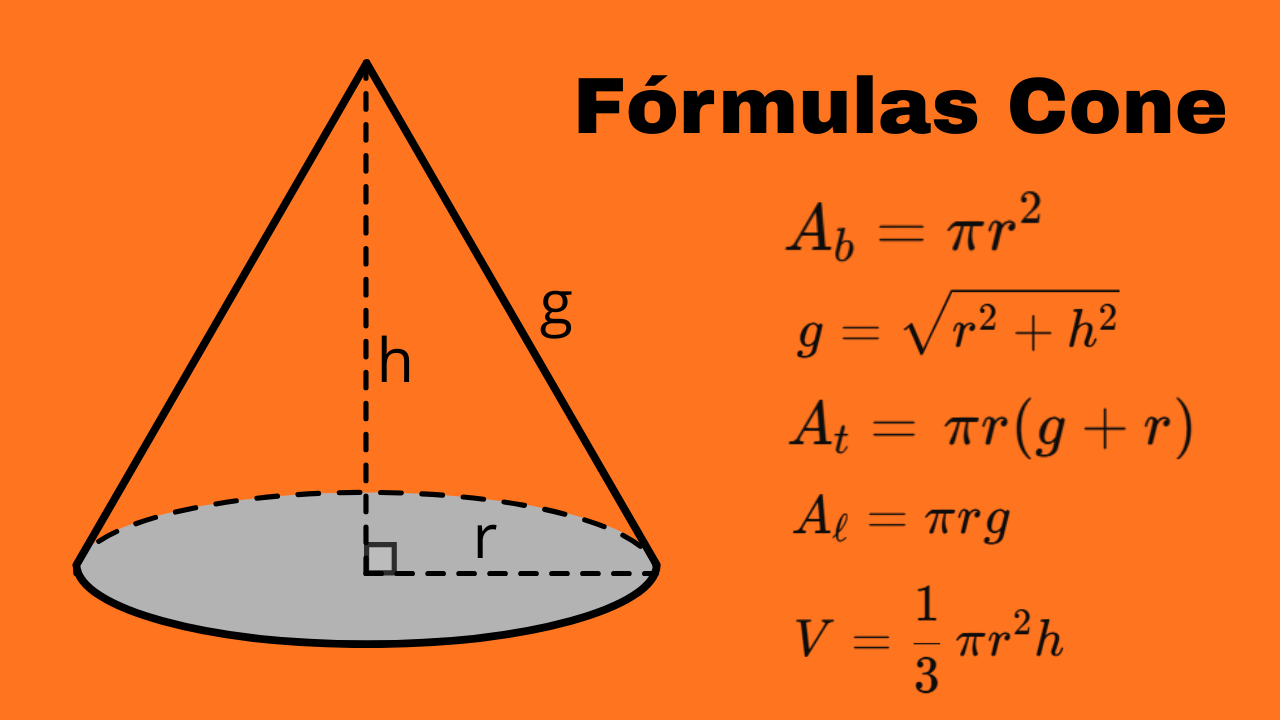
O cone é um dos principais corpos redondos. Aqui você encontra todas as fórmulas do cone circular reto, com exemplos passo a passo. Para comparar com outros sólidos: esfera, cubo, paralelepípedo. Para mais prática geral com sólidos, veja exercícios de esfera.
Notação
- \(r\): raio da base (círculo) — diâmetro \(d=2r\);
- \(h\): altura (distância do vértice ao centro da base — perpendicular ao plano da base);
- \(g\): geratriz (lado inclinado). Para cone reto: \( \displaystyle g=\sqrt{r^{2}+h^{2}} \).
Fórmulas principais
Planificação (ângulo do setor)
Ao “abrir” a lateral, obtemos um setor circular de raio \(g\) e arco \(2\pi r\). Logo, o ângulo do setor é
Tronco do cone (bônus)
Se o cone é cortado por um plano paralelo à base (raios \(r_1>r_2\), altura \(h\)), com \( \displaystyle g=\sqrt{(r_1-r_2)^2+h^2} \):
- Área lateral: \( \displaystyle A_\ell=\pi(r_1+r_2)\,g \)
- Área total: \( \displaystyle A_t=A_\ell+\pi r_1^2+\pi r_2^2 \)
- Volume: \( \displaystyle V=\frac{1}{3}\pi h\,(r_1^2+r_1r_2+r_2^2) \)
Exemplos resolvidos (passo a passo, um por linha)
Exemplo 1 — do clássico 3-4-5. Dado \(r=3\ \text{cm}\) e \(h=4\ \text{cm}\), calcule \(g\), \(A_\ell\), \(A_t\) e \(V\).
Exemplo 2 — ângulo da planificação. Um cone tem \(r=4\ \text{cm}\) e \(g=10\ \text{cm}\). Encontre o ângulo do setor em graus.
Exemplo 3 — tronco do cone. Para \(r_1=6\ \text{cm}\), \(r_2=4\ \text{cm}\), \(h=8\ \text{cm}\):
Exercícios rápidos (múltipla escolha com solução)
1) Num cone com \(r=5\ \text{cm}\) e \(h=12\ \text{cm}\), calcule \(g\) e \(A_\ell\).
- \(g=12,\ A_\ell=60\pi\)
- \(g=13,\ A_\ell=65\pi\)
- \(g=13,\ A_\ell=60\pi\)
- \(g=12,\ A_\ell=65\pi\)
Ver solução
Resposta: B.
2) Um cone tem \(d=10\ \text{cm}\) e \(h=12\ \text{cm}\). A área total é:
- \(80\pi\)
- \(85\pi\)
- \(90\pi\)
- \(95\pi\)
Ver solução
Resposta: C.
3) Se multiplicarmos \(r\) e \(h\) por 3, o volume do cone fica:
- 3 vezes maior
- 6 vezes maior
- 9 vezes maior
- 27 vezes maior
Ver solução
Resposta: D.
Erros comuns & dicas
- Trocar \(g\) por \(h\) em \(A_\ell=\pi r g\).
- Volume sempre usa \(h\) (altura) e não a geratriz.
- Unidades: área em cm²/m²; volume em cm³/m³.
- Se derem apenas \(g\) e \(r\), obtenha \(h=\sqrt{g^{2}-r^{2}}\).
Leituras relacionadas (linkagem interna)
- Corpos redondos — panorama (cilindro, cone, esfera…).
- Esfera — área e volume.
- Cubo e Paralelepípedo — comparação com poliedros.
- Prática extra: Exercício Esfera.





















