Relação Fundamental do Triângulo Retângulo
A relação fundamental da trigonometria é uma identidade que conecta o seno e o cosseno de um ângulo agudo de um triângulo retângulo. Essa relação é essencial para a resolução de problemas de geometria, trigonometria e até de física.
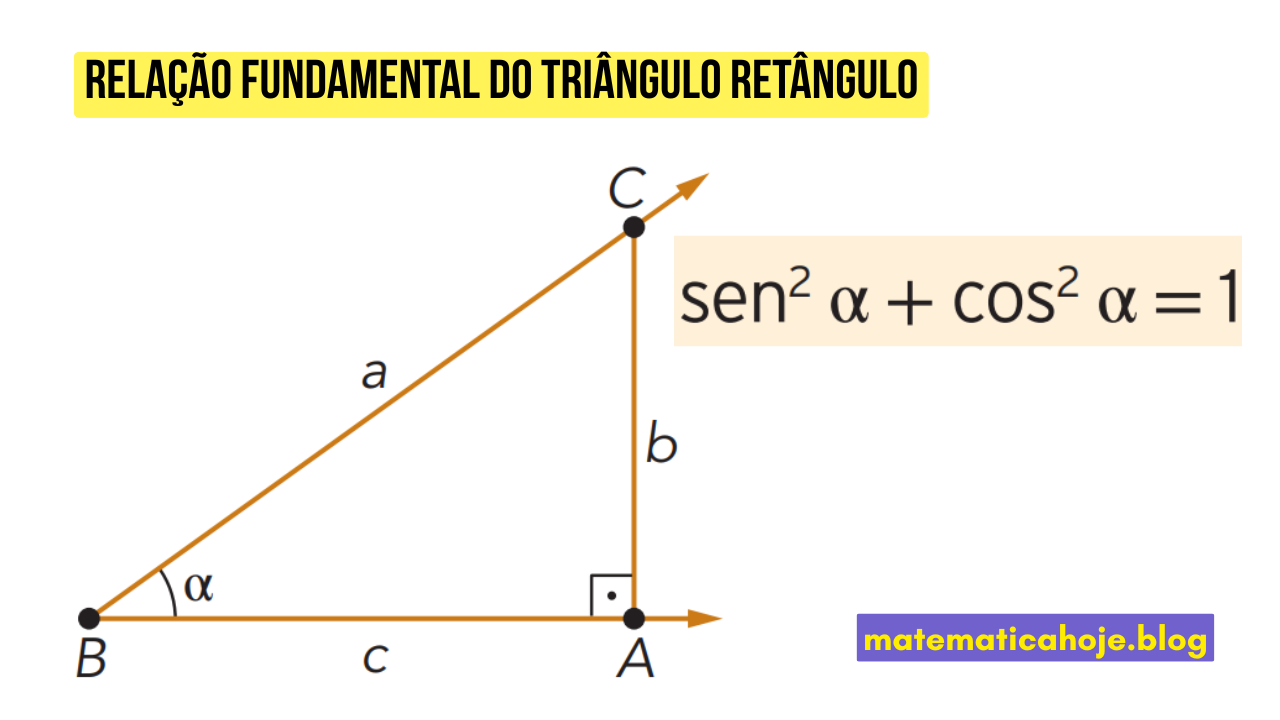
Definição
Seja um triângulo retângulo com ângulo agudo \(\alpha\), temos:
Demonstração
Num triângulo retângulo \(ABC\), com hipotenusa \(a\) e catetos \(b\) e \(c\):
- \(\sin \alpha = \frac{b}{a}\)
- \(\cos \alpha = \frac{c}{a}\)
Então:
Pelo Teorema de Pitágoras: \(a^2 = b^2 + c^2\). Assim:
Exemplo Resolvido
Exemplo: Se \(\cos \alpha = \frac{4}{5}\), calcule \(\sin \alpha\).
Pela relação fundamental: \(\sin^2 \alpha + \left(\frac{4}{5}\right)^2 = 1\).
\(\sin^2 \alpha + \frac{16}{25} = 1 \Rightarrow \sin^2 \alpha = \frac{9}{25}\).
\(\sin \alpha = \frac{3}{5}\).
📘 Exercícios de Múltipla Escolha
1) Se \(\sin \alpha = \frac{5}{13}\), então \(\cos \alpha =\)
- \(\frac{12}{13}\)
- \(\frac{12}{13}\)
- \(\frac{5}{12}\)
- \(\frac{13}{12}\)
Ver solução
\(\cos^2 \alpha = 1 – \sin^2 \alpha = 1 – \left(\frac{25}{169}\right) = \frac{144}{169}\).
\(\cos \alpha = \frac{12}{13}\).
2) Se \(\cos \alpha = 0,6\), determine \(\sin \alpha\).
- \(0,6\)
- \(0,8\)
- \(0,9\)
- \(0,75\)
Ver solução
\(\sin^2 \alpha = 1 – (0,6)^2 = 1 – 0,36 = 0,64\).
\(\sin \alpha = 0,8\).
3) Se \(\sin \alpha = \frac{7}{25}\), qual o valor de \(\cos^2 \alpha\)?
- \(\frac{49}{625}\)
- \(\frac{576}{625}\)
- \(\frac{25}{49}\)
- \(\frac{24}{25}\)
Ver solução
\(\sin^2 \alpha = \frac{49}{625}\). Logo, \(\cos^2 \alpha = 1 – \frac{49}{625} = \frac{576}{625}\).
Links para aprofundar
📚 Produtos Recomendados
Estude trigonometria e outros conteúdos de geometria com nossos materiais exclusivos:





















