Circunferência Trigonométrica
A circunferência trigonométrica é a circunferência orientada com centro na origem do sistema de coordenadas cartesianas ortogonais, cujo raio tem medida 1 unidade. O sentido positivo é o anti-horário, e ela é a base de toda a trigonometria no plano.
Definição
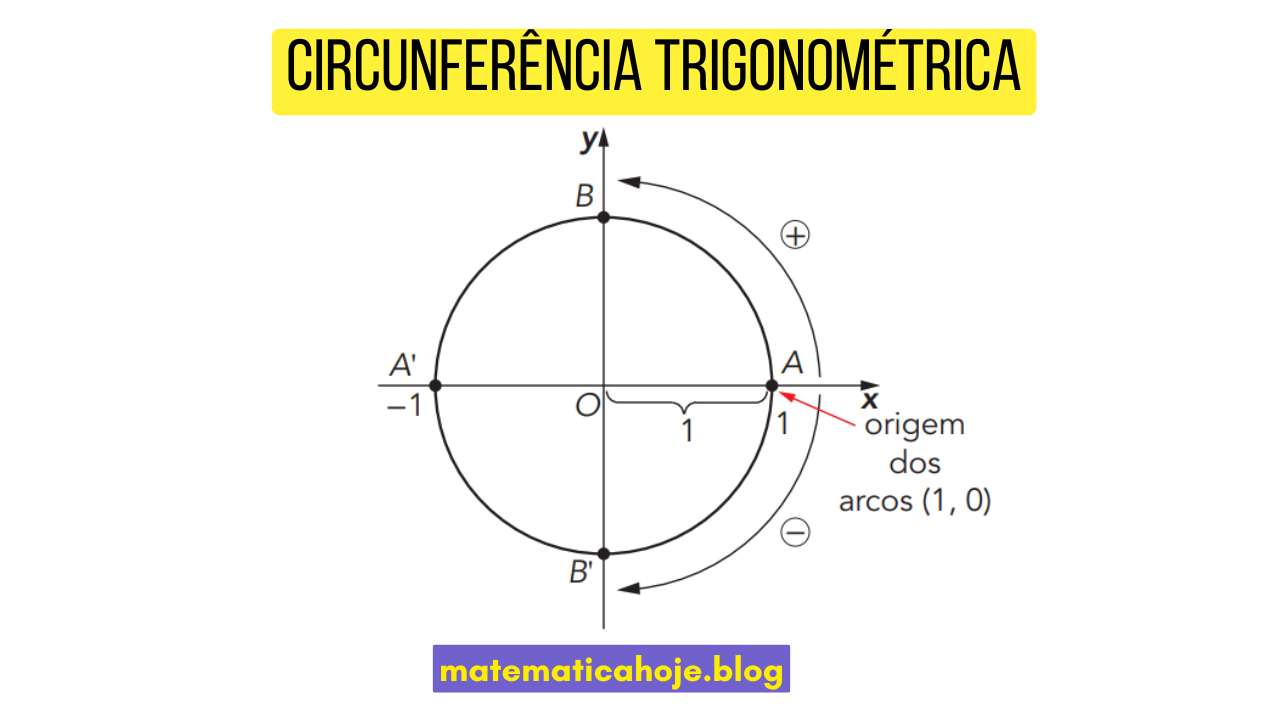
A circunferência trigonométrica é usada para representar ângulos, senos, cossenos e tangentes de forma geométrica. O ponto inicial, chamado de origem dos arcos, é o ponto \(A(1,0)\) no eixo \(x\).
Propriedades importantes
- O raio mede sempre 1 unidade.
- O movimento no sentido anti-horário corresponde a ângulos positivos, e no horário, a ângulos negativos.
- Os pontos da circunferência têm coordenadas \((\cos \theta, \sin \theta)\), sendo \(\theta\) o ângulo correspondente.
- A tangente de um ângulo pode ser obtida pela razão entre as coordenadas: \( \tan \theta = \frac{\sin \theta}{\cos \theta} \).
Exemplo resolvido
Exemplo:
Determine as coordenadas do ponto da circunferência trigonométrica associado ao ângulo de \(60^\circ\).
Solução:
As coordenadas são dadas por:
\((\cos 60^\circ, \sin 60^\circ) = \left(\tfrac{1}{2}, \tfrac{\sqrt{3}}{2}\right)\).
Portanto, o ponto correspondente é \(\left(\tfrac{1}{2}, \tfrac{\sqrt{3}}{2}\right)\).
📘 Exercícios de múltipla escolha
1) O ponto da circunferência trigonométrica correspondente a \(90^\circ\) é:
- \((1,0)\)
- \((0,1)\)
- \((-1,0)\)
- \((0,-1)\)
Ver solução
No ângulo de \(90^\circ\), temos \(\cos 90^\circ = 0\) e \(\sin 90^\circ = 1\). Correto: B.
2) O ponto da circunferência associado a \(180^\circ\) é:
- \((0,1)\)
- \((1,0)\)
- \((-1,0)\)
- \((0,-1)\)
Ver solução
\(\cos 180^\circ = -1\), \(\sin 180^\circ = 0\). Correto: C.
Links relacionados
📚 Continue estudando
A circunferência trigonométrica é essencial para entender a geometria dos ângulos e funções trigonométricas no plano cartesiano.





















