Definição de Função

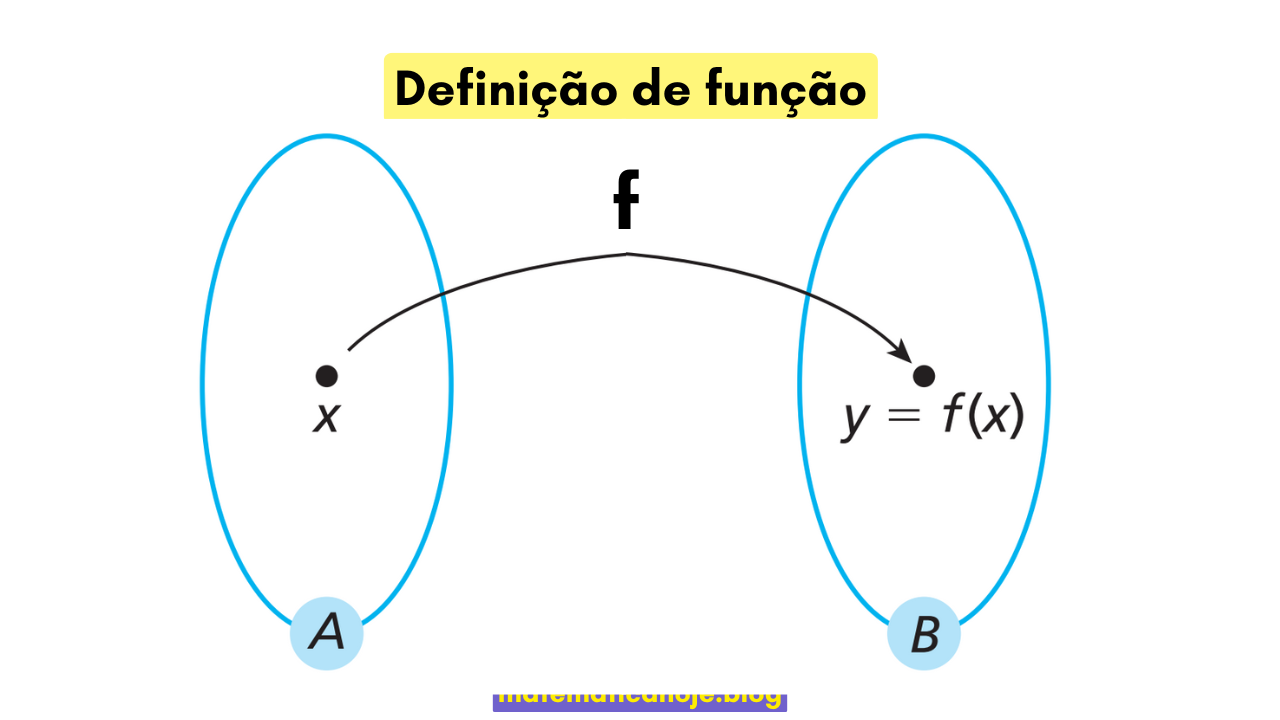
Na figura a seguir, um elemento \(x\) do conjunto \(A\) é enviado por uma regra \(f\) a um elemento \(y=f(x)\) do conjunto \(B\). Essa é a essência do conceito de função.

Definição formal. Uma função \(f: A \to B\) é uma regra que associa, para cada \(x\in A\), um único \(y\in B\). Escrevemos \(y=f(x)\).

Vocabulário essencial

Domínio (\(A\)): conjunto de entrada.
Contradomínio (\(B\)): conjunto de saída possível.
Imagem \(\mathrm{Im}(f)\): valores efetivamente obtidos em \(B\).
Representações: lei de formação, tabela, pares ordenados e diagrama de setas.

Leituras relacionadas

Conjuntos Numéricos • Função do 2º Grau • Equações do 1º Grau • Logaritmos • Operações com Frações

📘 Reforço para a prova: veja o eBook Fórmulas Matemática para ter as principais fórmulas de funções sempre à mão.

Exemplos rápidos

Exemplo 1 — Lei de formação

Se \(f:\mathbb{R}\to\mathbb{R}\) é dada por \(f(x)=2x-3\), então \(f(4)=5\) e \(f(-1)=-5\). A imagem de todo real é um real: função bem definida.

Exemplo 2 — Tabela em conjunto finito

\(x\in A=\{0,1,2,3\}\)	\(f(x)=x^2+1\)
0	1
1	2
2	5
3	10

Imagem: \(\{1,2,5,10\}\).

Exemplo 3 — Relação que não é função

Se \(R=\{(a,1),(a,2),(b,3)\}\) com domínio \(\{a,b\}\), o elemento \(a\) tem duas imagens ⇒ não é função.

Praticar no Banco de Questões

Exercícios com solução

1) Seja \(f:\mathbb{R}\to\mathbb{R}\) dada por \(f(x)=3x+2\). Determine \(f(-2)\) e \(f(0)\).

Ver solução

\(f(-2)=3(-2)+2=-6+2=-4\)
\(f(0)=3(0)+2=2\)

2) Em \(A=\{-2,-1,0,1,2\}\), considere \(g(x)=x^2\). Calcule \(\mathrm{Im}(g)\).

Ver solução

\(g(-2)=4,\; g(-1)=1,\; g(0)=0,\; g(1)=1,\; g(2)=4\)
Distintos: \(\{0,1,4\}\).

3) A relação \(H=\{(1,2),(1,3),(2,4)\}\) em \(A=\{1,2\}\) e \(B=\{2,3,4\}\) é função de \(A\) em \(B\)? Justifique.

Ver solução

Não é função: o elemento \(1\in A\) tem duas imagens (2 e 3).

4) Seja \(p:A\to B\) com \(A=\{0,1,2,3\}\) e \(p(x)=2x+1\). Escreva os pares ordenados de \(p\) e a imagem.

Ver solução

\(p(0)=1,\; p(1)=3,\; p(2)=5,\; p(3)=7\)
Pares: \(\{(0,1),(1,3),(2,5),(3,7)\}\)
Imagem: \(\{1,3,5,7\}\).

5) Defina \(q:\mathbb{Z}\to\mathbb{Z}\) por \(q(x)=\begin{cases}x/2,&\text{se }x\text{ é par}\\ 3x+1,&\text{se }x\text{ é ímpar}\end{cases}\). Calcule \(q(\,-3),\, q(0),\, q(4)\).

Ver solução

\(-3\) é ímpar ⇒ \(q(-3)=3(-3)+1=-9+1=-8\)
\(0\) é par ⇒ \(q(0)=0/2=0\)
\(4\) é par ⇒ \(q(4)=4/2=2\)