Estudo do sinal de uma função
Como descobrir onde \(f(x)\) é positiva, negativa ou nula. Ideal para resolver desigualdades.
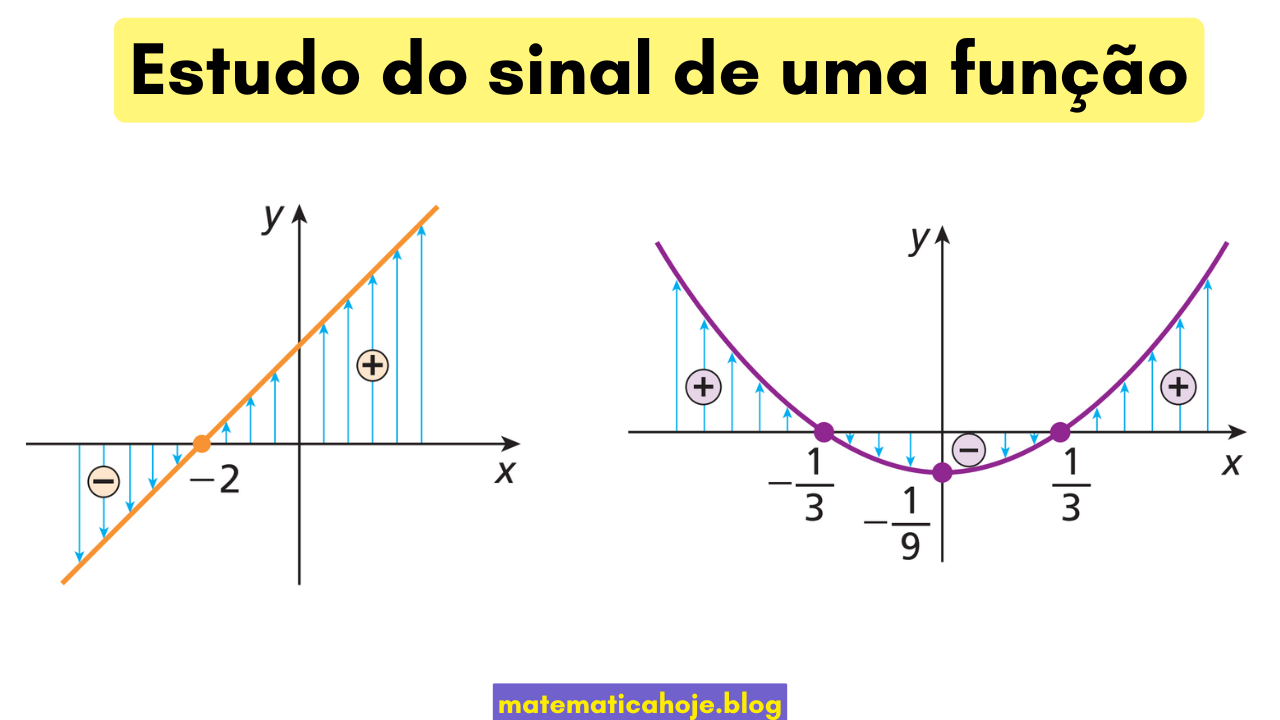
O que é “sinal” de uma função?
Para uma função \(f\), dizemos que:
- \(f(x)>0\) (positiva) quando os pontos do gráfico estão acima do eixo \(x\);
- \(f(x)<0\) (negativa) quando estão abaixo do eixo \(x\);
- \(f(x)=0\) (nula) nos zeros ou raízes da função (interseções com o eixo \(x\)).
Estudar o sinal é base para resolver desigualdades como \(f(x)\ge0\), \(f(x)<0\), etc. Veja também: Zero de uma função, Gráfico de uma Função e Domínio e Imagem.
Procedimento geral (quadro de sinais)
- Domínio — determine onde \(f\) está definida.
- Zeros/pontos críticos — resolva \(f(x)=0\) (e, se racional, anote também onde o denominador zera).
- Ordene os pontos na reta real: \(x_1
- Teste intervalos (um ponto em cada intervalo) ou use as regras de multiplicidade:
- Raiz de multiplicidade ímpar (fator \((x-a)^m\) com \(m\) ímpar) troca o sinal ao passar por \(x=a\).
- Raiz de multiplicidade par não troca o sinal.
- Em racionais, zeros do numerador e polos (zeros do denominador) também podem trocar o sinal conforme as multiplicidades.
- Monte o quadro e conclua onde \(f(x)\gtrless 0\). Inclua ou exclua os pontos conforme \(\ge,\le,>,<\).
- Teste intervalos (um ponto em cada intervalo) ou use as regras de multiplicidade:
Exemplos resolvidos
1) Função afim
\(f(x)=2x+4\). Zero em \(2x+4=0\Rightarrow x=-2\).
Sinal: para \(x<-2\), \(f(x)<0\); para \(x>-2\), \(f(x)>0\). Logo: \[ f(x)\ge0 \iff x\ge -2,\qquad f(x)<0 \iff x<-2. \]
2) Quadrática simples
\(g(x)=x^2-\dfrac{1}{9}\). Zeros: \(x=\pm\dfrac{1}{3}\).
Como a concavidade é para cima, \(g(x)<0\) entre as raízes e \(>0\) fora:
\[
g(x)<0 \iff -\tfrac13 \(h(x)=(x-1)^2(x+2)\). Raízes: \(x=1\) (multiplicidade 2) e \(x=-2\) (multiplicidade 1). O sinal troca em \(x=-2\) e não troca em \(x=1\).
Se testar \(x\to+\infty\), \(h(x)>0\). Caminhando para a esquerda:
\(r(x)=\dfrac{(x-1)(x+2)}{x-3}\). Domínio: \(\mathbb{R}\setminus\{3\}\). Pontos: zeros \(x=1,-2\); pólo \(x=3\). Organizando: \(-\infty < -2 < 1 < 3 < +\infty\). Tomando um ponto por intervalo ou multiplicidades:
3) Multiplicidade
\((1,+\infty)\): \(+\) → ao passar por \(1\) (par) mantém \(+\).
\((-2,1)\): \(+\) → ao passar por \(-2\) (ímpar) inverte para \( – \).
\((-\infty,-2)\): \( – \).
4) Função racional
Logo \(r(x)>0\) em \((-2,1)\cup(3,\infty)\) e \(r(x)<0\) em \((-\infty,-2)\cup(1,3)\).
Quadro-resumo rápido
| Situação | O que acontece com o sinal? | Dica |
|---|---|---|
| Raiz com expoente ímpar | Troca o sinal ao atravessar a raiz | Fator \((x-a)^{2k+1}\) |
| Raiz com expoente par | Não troca o sinal | Fator \((x-a)^{2k}\) |
| Pólo (denominador zero) | Geralmente há troca, conforme multiplicidade | Não pertence ao domínio |
| Produto de fatores | Par de negativos → positivo; ímpar → negativo | Conte os “menos” |
| Quociente \(N/D\) | Sinal é o de \(N\) multiplicado pelo de \(D\) | Analise separadamente |
Exercícios (múltipla escolha) com solução
1) O conjunto solução de \(2x+6\ge0\) é:
- \((-\infty,-3)\)
- \((-\infty,-3]\)
- \([-3,\infty)\)
- \((-3,\infty)\)
Ver solução
2) Resolva \(x^2-\dfrac{1}{9}<0\).
- \(x\in\mathbb{R}\)
- \(x\in(-\tfrac13,\tfrac13)\)
- \(x\in(-\infty,-\tfrac13)\cup(\tfrac13,\infty)\)
Ver solução
3) Para \(h(x)=(x-1)^2(x+2)\), o sinal em \(x=1\) e seus arredores é:
- Muda de \(+\) para \(-\)
- Permanece o mesmo
- Indeterminado
Ver solução
4) Para \(r(x)=\dfrac{(x-1)(x+2)}{x-3}\), assinale onde \(r(x)>0\).
- \((-\infty,-2)\cup(1,3)\)
- \((-2,1)\cup(3,\infty)\)
- \((-2,1)\cup(1,3)\)
Ver solução
5) Inequação: \(\dfrac{x-4}{(x+1)^2}\le0\). O conjunto solução é:
- \((-\infty,-1)\cup(-1,4]\)
- \((-\infty,-1)\cup[4,\infty)\)
- \((-\infty,4]\setminus\{-1\}\)
Ver solução
6) Para \(p(x)=(x-2)^3(x+5)\), o sinal ao cruzar \(x=2\) é:
- Não muda
- Muda
- Depende do outro fator
Ver solução
Links internos e materiais do blog
• Zeros de função •
Gráfico de uma função •
Funções injetiva/sobrejetiva/bijetiva
• Produtos: Mapas Mentais •
ENEM Matemática •
Coleção 10 eBooks •
Banco de Questões •
eBook Fórmulas Matemática





















