Em geometria, entender retas paralelas é fundamental para resolver problemas de ângulos, construir figuras geométricas e interpretar situações do dia a dia, como a marcação das faixas de pedestre, trilhos de trem ou fileiras de carteiras em uma sala de aula. Neste artigo, vamos caminhar com calma, como se estivéssemos em sala, analisando passo a passo a imagem abaixo e descobrindo a relação entre os ângulos formados.
1. O que são retas paralelas?
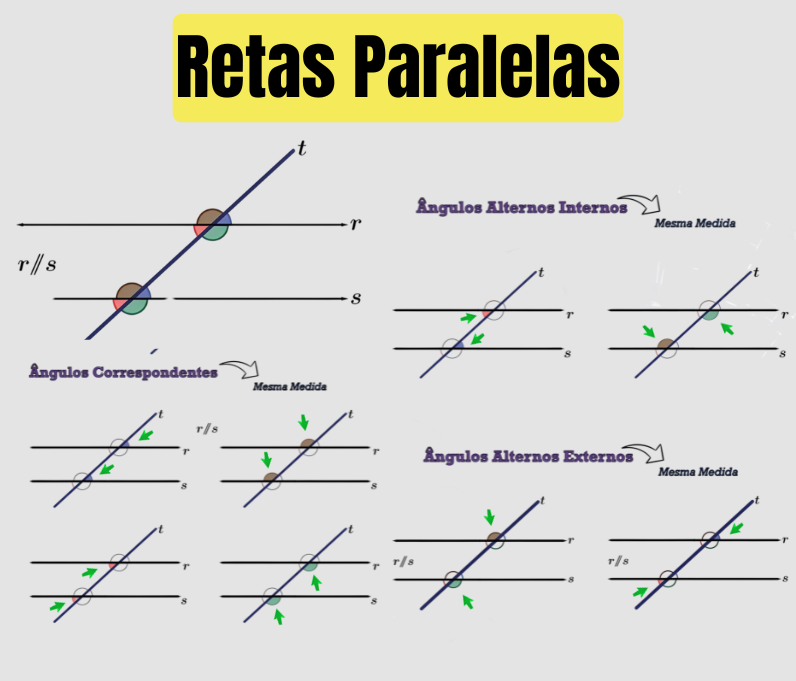
Observe que, na parte principal da imagem, aparecem duas retas horizontais, chamadas de r e s, e uma reta inclinada, chamada de t. As retas r e s estão sempre à mesma distância uma da outra e nunca se encontram, por mais que sejam prolongadas. Por isso dizemos que r ∥ s (lê-se “r paralela a s”).
A reta inclinada t corta as duas retas paralelas. Ela recebe o nome de reta transversal. Sempre que uma transversal corta duas retas paralelas, aparecem vários ângulos que se relacionam entre si. É essa “família de ângulos” que vamos explorar agora.
Duas retas paralelas r e s são cortadas por uma transversal t. Em cada ponto de interseção, formam-se quatro ângulos. Como temos duas interseções, ao todo surgem oito ângulos. Toda a teoria que veremos a seguir organiza esses oito ângulos em pares especiais (correspondentes, alternos internos, alternos externos etc.).
2. Entendendo os pares de ângulos na figura
Repare que, ao cruzar a reta r, a transversal t forma quatro ângulos. O mesmo acontece quando ela cruza a reta s. Assim, ao todo, temos oito ângulos. Alguns estão pintados com as mesmas cores na imagem, indicando que possuem a mesma medida.
Imagine, por exemplo, que um dos ângulos formados em r seja de 120°. Sem precisar de transferidor, conseguimos descobrir diversos outros ângulos iguais a ele apenas pela posição. É exatamente isso que os nomes correspondentes, alternos internos e alternos externos nos ajudam a organizar.
3. Ângulos correspondentes: “mesma posição” nas retas paralelas
Observe, na parte inferior esquerda da imagem, o bloco com o título Ângulos Correspondentes. As setas verdes indicam pares de ângulos que ocupam posições muito parecidas em relação às retas r, s e à transversal t.
Dizemos que dois ângulos são correspondentes quando estão:
- no mesmo lado da transversal;
- ambos “acima” das retas ou ambos “abaixo” das retas;
- em posições “espelhadas” nas duas interseções.
Em outras palavras, se você “deslizasse” a reta r até a posição da reta s, o ângulo correspondente “cairia” exatamente sobre o outro.
Propriedade importante: se as retas r e s são paralelas, então os ângulos correspondentes têm a mesma medida. É o que a imagem destaca com a frase “Mesma Medida”.
Em um desenho, as retas r e s são paralelas e uma transversal t forma, na interseção com r, um ângulo de 65° na região superior e à direita. Na interseção com s, o ângulo que fica também na parte superior e à direita da transversal é correspondente.
Como as retas são paralelas, concluímos que esse ângulo mede também 65°. Mesmo sem medir com transferidor, a geometria garante essa igualdade.
Vamos praticar como se estivéssemos em sala: suponha que um dos ângulos correspondentes na reta r meça 65°. Pare um instante e tente descobrir, sem olhar mais nada, quanto mede o ângulo correspondente na reta s. Resposta: também mede 65°, justamente porque as retas são paralelas.
4. Ângulos alternos internos: dentro do “corredor” entre as paralelas
Agora, olhe para o bloco da direita superior, com o título Ângulos Alternos Internos. As setas verdes apontam para dois ângulos que estão dentro da região entre as retas r e s. Por isso são chamados de internos.
Eles também ficam em lados opostos da transversal t. Essa mudança de lado é o que chamamos de alternos.
Assim, dois ângulos são chamados de alternos internos quando:
- estão entre as duas retas paralelas;
- ficam em lados opostos da transversal;
- não ocupam exatamente a mesma posição (um fica “de um lado”, outro “do outro”).
Outra vez, a imagem traz a anotação “Mesma Medida”, reforçando a propriedade: quando r ∥ s, os ângulos alternos internos são congruentes, isto é, possuem a mesma medida.
Suponha que, entre as retas r e s, um dos ângulos formados pela transversal t mede 110°. Ele está à esquerda da transversal. O ângulo que está à direita da transversal, também entre r e s, é alterno interno em relação ao primeiro.
Como as retas são paralelas, esse outro ângulo também mede 110°. Se uma questão pedir a medida dele, basta reconhecer o par de alternos internos.
Experimente um exercício mental: se um dos ângulos alternos internos mede 110°, qual é a medida do outro? Ao reconhecer o par alterno interno, concluímos que também é 110°. É com esse tipo de raciocínio que resolvemos vários problemas de provas de concurso, vestibulares e exames como o ENEM, muitas vezes sem precisar fazer contas longas.
5. Ângulos alternos externos: fora do corredor, mas com o mesmo raciocínio
Na parte inferior direita da imagem aparecem os Ângulos Alternos Externos. A lógica é a mesma dos alternos internos, porém agora os ângulos estão fora da região entre as retas paralelas, isto é, na parte de cima da reta r ou na parte de baixo da reta s.
Dois ângulos são alternos externos quando:
- ficam fora da região entre as duas paralelas;
- estão em lados opostos da transversal;
- formam um par “cruzado”, semelhante ao caso interno, mas na região externa.
A propriedade destacada na figura se repete: se as retas são paralelas, os ângulos alternos externos têm a mesma medida.
Considere que, acima da reta r, à direita da transversal, existe um ângulo de 45°. Abaixo da reta s, à esquerda da transversal, há outro ângulo que forma um par alterno externo com o primeiro.
Como as retas são paralelas, esse segundo ângulo também mede 45°. Em problemas de engenharia simples, esse tipo de raciocínio garante simetria em vigas e rampas.
Imagine a seguinte situação prática, muito parecida com os exercícios de livros didáticos: em um esquema de passarela elevada, duas rampas laterais fazem o papel de retas paralelas, e uma escada transversal liga os níveis. Se um ângulo externo formado por uma rampa e a escada mede 45°, o ângulo alterno externo, do outro lado da escada, também medirá 45°. Isso garante que o desenho esteja coerente e que a estrutura seja simétrica.
6. Como essas ideias aparecem em problemas e exercícios
Quando resolvemos questões de geometria, raramente o enunciado diz claramente “calcule o ângulo alterno interno”. O que mais acontece é o problema descrever uma situação com trilhos, ruas ou vigas paralelas, mencionar apenas a medida de um dos ângulos e pedir outra medida “escondida” no desenho.
Veja um exemplo típico que você pode treinar agora mesmo: duas retas paralelas são cortadas por uma transversal. Um dos ângulos correspondentes é reto, isto é, mede 90°. Qual é a medida de:
a) o ângulo correspondente a ele na outra reta?
b) o ângulo alterno interno associado?
c) um ângulo suplementar a esse de 90° na mesma
interseção?
Sabemos que um ângulo correspondente mede 90°.
a) Como os correspondentes são iguais, o ângulo correspondente na outra reta também mede 90°.
b) O alterno interno que faz par com esse ângulo, por serem retas paralelas, também mede 90°.
c) Ângulos suplementares somam 180°. Assim, o ângulo suplementar a 90° mede 180° − 90° = 90°.
Nesse exemplo, três ângulos diferentes do desenho acabam tendo a mesma medida apenas pelas relações de paralelismo.
Raciocinando com calma: na letra (a), por serem correspondentes e as retas serem paralelas, o outro ângulo também mede 90°. Na letra (b), o alterno interno que faz par com um ângulo reto também será 90°. Já na letra (c), se dois ângulos são suplementares, suas medidas somam 180°, logo o outro mede 90° (pois 90° + 90° = 180°). Em poucas linhas, usamos correspondentes, alternos e suplementares de forma combinada, como acontece nas provas.
7. Propriedade recíproca: quando os ângulos garantem o paralelismo
Até aqui, partimos da ideia de que as retas já são paralelas e concluímos que certos pares de ângulos têm a mesma medida. Porém, em muitos problemas mais desafiadores, o raciocínio vai na direção contrária: se dois ângulos correspondentes (ou alternos internos, ou alternos externos) possuem a mesma medida, então podemos concluir que as duas retas são paralelas.
Em um desenho, duas retas cortadas por uma transversal formam um par de ângulos alternos internos de 130° cada. Se o problema não disser explicitamente que as retas são paralelas, a igualdade desses alternos internos é suficiente para concluir que elas são, sim, paralelas. É a aplicação prática da propriedade recíproca.
Por exemplo, se em um desenho de telhado você descobre que um par de ângulos alternos internos é igual a 130° e outro também mede 130°, essa igualdade é um forte argumento para afirmar que as vigas desenhadas foram projetadas paralelamente. Essa ideia é muito usada tanto em demonstrações geométricas quanto em problemas de engenharia e arquitetura.
8. Retas paralelas, percepção espacial e provas
Dominar as relações entre ângulos correspondentes, alternos internos e alternos externos melhora muito a percepção espacial do estudante. Em exercícios de interpretação de gráficos, construção de polígonos e questões de simetria, esses conceitos aparecem de forma discreta, mas decisiva. Em exames que cobram bastante geometria, como concursos públicos e o ENEM, enxergar rapidamente as retas paralelas pode fazer você ganhar tempo precioso.
Uma boa estratégia é treinar com bastante variedade de figuras: algumas bem parecidas com a imagem deste artigo, outras mais “escondidas” em polígonos, trapézios ou em desenhos de ruas que se cruzam. Assim, você não fica dependente de um único tipo de exercício e se prepara melhor para o que pode aparecer nas provas.
Se quiser um apoio extra com listas de exercícios organizadas por assunto, vale a pena conhecer os materiais do blog, como bancos de questões, simulados e revisões específicas para provas de Matemática.













