Nesta questão do ENEM 2025, trabalhamos conceitos de volume do cilindro, prisma de base quadrada e subtração de volumes. O objetivo é determinar o volume de ouro necessário para a fabricação de medalhas comemorativas.
Distância percorrida em partida de futebol – ENEM 2025
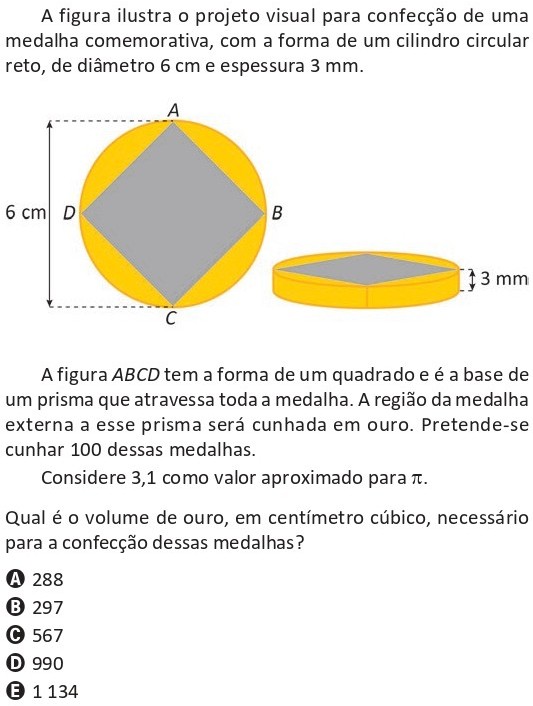
A medalha tem formato de cilindro circular reto, com diâmetro de 6 cm e espessura de 3 mm. Um prisma de base quadrada atravessa toda a medalha, e apenas a região externa a esse prisma será feita em ouro. Devem ser produzidas 100 medalhas, usando π ≈ 3,1.
Ver solução passo a passo
1) Conversão da espessura
A espessura é 3 mm.
Sabendo que 10 mm = 1 cm, temos:
3 mm = 3 ÷ 10 = 0,3 cm.
2) Raio do cilindro
O diâmetro da medalha é 6 cm, então o raio é a metade:
r = 6 ÷ 2 = 3 cm.
3) Volume do cilindro (medalha inteira)
Fórmula do volume do cilindro: Vcil = π · r² · h
Substituindo os valores:
r = 3 cm, h = 0,3 cm, π ≈ 3,1
r² = 3² = 9
Vcil = 3,1 · 9 · 0,3
3,1 · 9 = 27,9
27,9 · 0,3 = 8,37 cm³
Portanto, o volume da medalha inteira é:
Vcil = 8,37 cm³.
4) Lado do quadrado interno
O quadrado está inscrito no círculo de diâmetro 6 cm, isto é,
a diagonal do quadrado é igual ao diâmetro do círculo:
diagonal d = 6 cm.
Para um quadrado, vale: d = ℓ · √2, onde ℓ é o lado.
Então:
ℓ · √2 = 6
ℓ = 6 ÷ √2 = 3 · √2.
5) Área da base quadrada
Área do quadrado: A = ℓ²
ℓ = 3 · √2
A = (3 · √2)² = 3² · (√2)² = 9 · 2 = 18 cm².
6) Volume do prisma interno
O prisma tem a mesma espessura da medalha (0,3 cm) e base quadrada de área 18 cm²:
Vprisma = área da base · altura
Vprisma = 18 · 0,3 = 5,4 cm³.
7) Volume de ouro em uma medalha
O ouro ocupa apenas a parte da medalha que sobra depois de retirar o volume do prisma interno:
Vouro (1 medalha) = Vcil – Vprisma
Vouro = 8,37 – 5,4 = 2,97 cm³.
8) Volume de ouro para 100 medalhas
Para 100 medalhas, basta multiplicar por 100:
Vtotal = 100 · 2,97 = 297 cm³.

























