A área do triângulo é a medida da região interna da figura. O segredo é escolher a fórmula certa de acordo com os dados que o problema fornece.
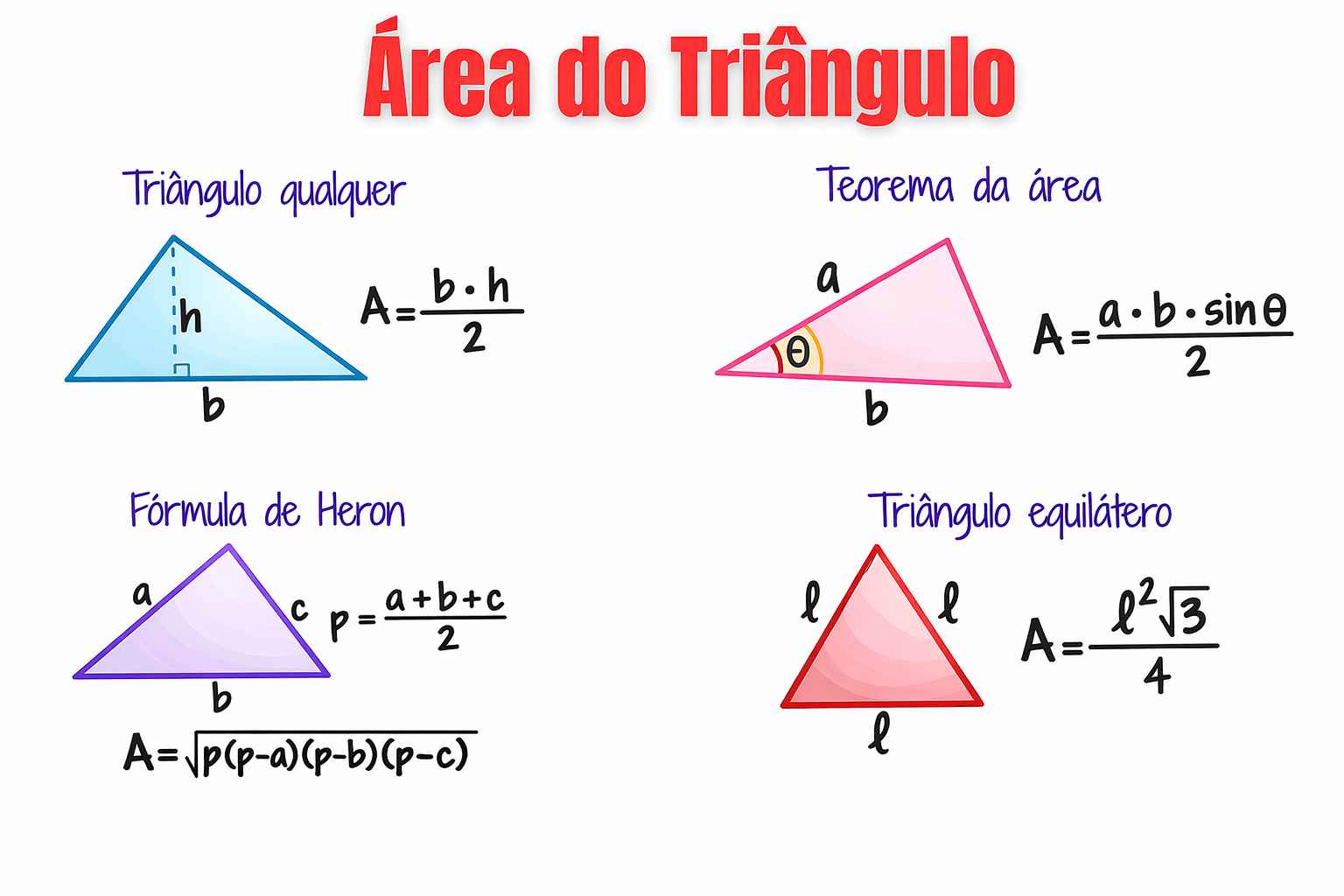
1) Triângulo qualquer (base e altura)
Use quando você conhece a base (b) e a altura (h) relativa a essa base (altura é perpendicular).
Unidade: se b e h estão em cm, a área sai em cm².
Exercício (base e altura)
Enunciado: Um triângulo tem base 18 cm e altura 7 cm. Calcule a área.
Ver solução (abre/fecha) ▾
Resposta: 63 cm².
2) Teorema da área (dois lados e o seno do ângulo)
Use quando você tem dois lados (a e b) e o ângulo entre eles (θ).
O ângulo precisa ser o ângulo entre os dois lados usados na fórmula.
Exercício (seno)
Enunciado: Em um triângulo, a = 12 cm, b = 9 cm e θ = 60°. Calcule a área.
Ver solução (abre/fecha) ▾
Resposta: 27√3 cm².
3) Fórmula de Heron (quando só tem os três lados)
Use quando o problema fornece apenas os lados a, b e c.
Exercício (Heron)
Enunciado: Um triângulo tem lados 7 cm, 8 cm e 9 cm. Calcule a área.
Ver solução (abre/fecha) ▾
Resposta: 12√5 cm².
4) Triângulo equilátero (fórmula direta)
Use quando o triângulo é equilátero e o lado é ℓ.
Exercício (equilátero)
Enunciado: Um triângulo equilátero tem lado ℓ = 10 cm. Calcule a área.
Ver solução (abre/fecha) ▾
Resposta: 25√3 cm².
Como escolher a fórmula certa (bem rápido)
- Base e altura → A = (b·h)/2
- Dois lados + ângulo entre eles → A = (a·b·senθ)/2
- Três lados → Heron
- Equilátero → A = (ℓ²·√3)/4













