O conceito de função matemática é um dos pilares da matemática. Ele aparece desde os primeiros conteúdos do Ensino Fundamental até provas de vestibulares, ENEM e concursos públicos. Apesar disso, muitos alunos sentem dificuldade porque o tema costuma ser apresentado de forma muito abstrata.
Neste guia, você vai entender o que é função de maneira simples, prática e visual, seguindo exatamente a lógica do mapa mental apresentado.
📌 Materiais do Matemática Hoje para acelerar seus estudos
Se você quer revisar com rapidez e ter um material pronto para consultar sempre que bater dúvida, confira estes conteúdos do Matemática Hoje:
Noção intuitiva de função
Antes de pensar em fórmulas, gráficos ou letras como x e y, precisamos compreender a ideia central de função.
👉 Uma função é uma relação que associa cada valor de uma grandeza a um único valor de outra grandeza.
Em outras palavras, quando uma coisa muda, a outra muda junto, seguindo uma regra. Essa relação é chamada de dependência.
Definição básica de função
Podemos resumir a definição básica de função em três ideias principais:
- Existe uma associação entre duas grandezas
- Há uma correspondência entre valores
- Uma grandeza depende da outra
Sempre que uma grandeza depende de outra, estamos diante de uma função.
Exemplo prático: preço de livros
Imagine a seguinte situação:
Cada livro custa R$ 70.
Se você compra:
- 1 livro → paga R$ 70
- 2 livros → paga R$ 140
- 3 livros → paga R$ 210
Observe que:
- A quantidade de livros pode variar → chamamos de x
- O preço total depende da quantidade → chamamos de y
📌 O preço total depende da quantidade de livros comprados.
✅ Quer aprender funções mais rápido?
Generalização matemática
Quando transformamos esse exemplo em linguagem matemática, usamos letras para representar as grandezas.
Nessa expressão:
- x representa a quantidade de livros
- y representa o preço total
Isso significa que o valor de y depende diretamente do valor de x.
Notação de função
Para deixar claro que existe uma relação de dependência, usamos a notação de função.
No exemplo dos livros:
As expressões y e f(x) representam exatamente o mesmo conceito: o valor que depende de x.
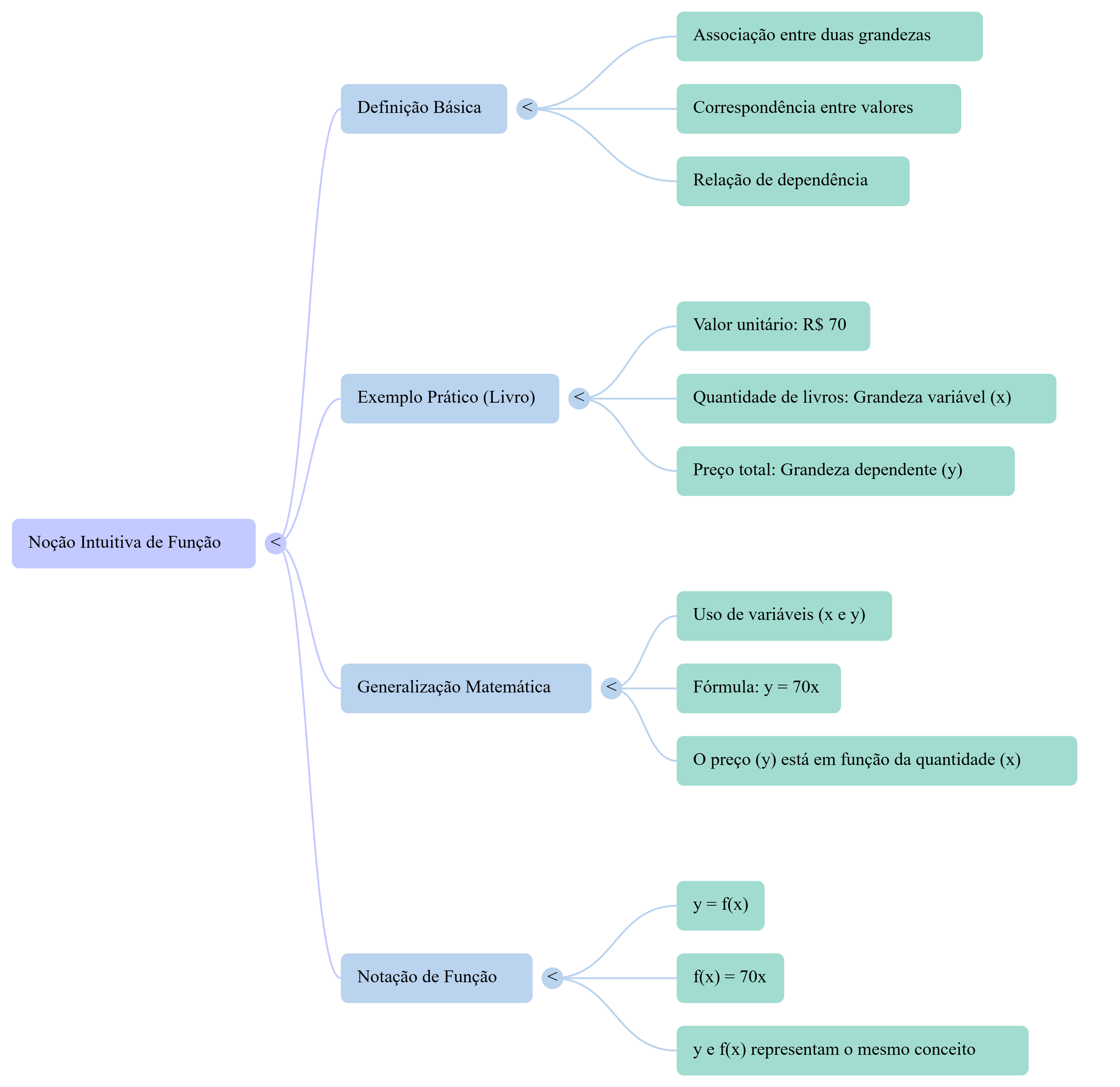
Resumo visual: mapa mental
Para facilitar a revisão, observe o mapa mental abaixo, que resume toda a ideia da introdução ao conceito de função.
Vídeo explicativo
Para reforçar o entendimento, assista ao vídeo abaixo com uma explicação clara e complementar sobre o conceito de função.
Agora que você entendeu a noção intuitiva de função, fica muito mais fácil avançar para gráficos, tipos de funções e aplicações em problemas e exercícios.













