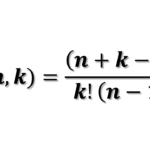Se você está se preparando para concursos, vestibulares ou o ENEM, dominar os fundamentos de Análise Combinatória é essencial. Neste post, reunimos 10 questões cuidadosamente selecionadas, numeradas de 1 a 10, todas com resolução comentada e explicação clara passo a passo. A proposta é não apenas apresentar o gabarito, mas ensinar o raciocínio por trás de cada resposta, ajudando você a fixar o conteúdo e ganhar confiança.
As questões abordam temas clássicos como permutação, combinação, princípio multiplicativo, entre outros, sempre com situações contextualizadas, como problemas de senhas, placas de veículos, provas escolares, distribuição de objetos, etc.
Aproveite para revisar, treinar e ampliar seu domínio sobre o assunto. No final da leitura, você estará muito mais preparado para enfrentar qualquer questão de combinatória que aparecer em sua prova!
Claro, Adriano! Abaixo está a lista reformulada das Questões 11 a 20, seguindo o padrão “Questão X: texto…” com melhoria nas explicações das soluções, pronta para ser publicada no blog:
Questão 1: Em uma instrução de orientação diurna, um aluno da Escola de Sargentos das Armas foi colocado na origem de um sistema cartesiano ortogonal. Considerando que ele dê exatamente 4 passos, um de cada vez, nas direções norte (N) ou leste (L), quantas trajetórias ele poderá percorrer?
a) 16
b) 36
c) 4
d) 12
e) 32
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Resposta: a) 16
Solução:
Cada passo tem 2 possibilidades: N ou L. Assim, para 4 passos, temos:
2×2×2×2 = 24 = 16
Logo, são 16 trajetórias diferentes possíveis.
[/toggle]
Questão 2: Um professor precisa elaborar uma prova multidisciplinar que consta de duas questões de Matemática e seis de Física. Ele deve escolher questões de um banco de dados que contém três questões de Matemática e oito de Física. O número de provas distintas possíveis, sem levar em conta a ordem em que as questões aparecem, é:
a) 42
b) 54
c) 62
d) 72
e) 84
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Resposta: e) 84
Solução:
Utilizamos combinação simples, pois a ordem das questões não importa.
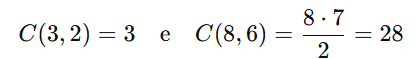
Multiplicando: 3×28 = 84
Portanto, há 84 provas distintas possíveis.
[/toggle]
Questão 3: Cinco estudantes (Daniela, Rafael, Renata, Gabriela e Lucas) farão parte da comissão de decoração de um evento. Quantas duplas diferentes podem ser formadas?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Resposta: 10
Solução:
Queremos o número de pares possíveis entre 5 pessoas. Usamos:
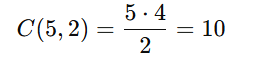
Ou seja, existem 10 duplas possíveis.
[/toggle]
Questão 4:A placa Mercosul é formada por três letras, um número, outra letra e dois algarismos, nessa ordem. Considerando que a placa comece por uma vogal e termine com o número 9, quantas placas podem ser formadas?
a) 6.083.500
b) 8.788.000
c) 79.092.000
d) 44.348.715
e) 175.760.000
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Resposta: b) 8.788.000
Solução:
- 5 vogais possíveis no início
- 26 letras para cada letra
- 10 algarismos para os números
- Último número fixado em 9 → 1 possibilidade
5⋅26⋅26⋅10⋅26⋅10⋅1 = 8.788.000
[/toggle]
Questão 5: Um painel de luzes pode ser configurado com cores primárias, intensidades e tipos de feixe. Também é possível acionar dois botões de cor para obter uma cor secundária, além das opções B (sem luz) e W (luz prateada). Qual o número total de possibilidades de iluminação?
a) 36
b) 38
c) 72
d) 110
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Resposta: b) 38
Solução:
- Cores primárias: 3 cores × 3 intensidades × 2 feixes = 18
- Cores secundárias: C(3,2) = 3 combinações × 3 × 2 = 18
- Botões B e W: 2
18+18+2 = 38 possibilidades
[/toggle]
Questão 6: Rafael tem uma estante com 10 livros distintos: 4 de História, 4 de Geografia e 2 de Biologia. De quantos modos diferentes ele pode arrumar os livros na estante, mantendo juntos os livros de cada disciplina?
a) 6.912
b) 3.456
c) 1.152
d) 1.150
e) 13.824
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Resposta: a) 6.912
Solução:
Cada grupo (disciplina) é tratado como um “bloco”:
- História: 4!
- Geografia: 4!
- Biologia: 2!
- 3 blocos → 3!
4!⋅4!⋅2!⋅3! = 24⋅24⋅2⋅6 = 6.912
[/toggle]
Questão 7: Considere os números:
x = 55, y = 6!, z = 172
Qual a ordem correta entre eles?
a) x < y < z
b) x < z < y
c) z < y < x
d) z < x < y
e) y < x < z
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Resposta: c) z < y < x
Solução:
- x = 3125
- y = 720
- z = 289
Portanto:
z < y < x
[/toggle]
Questão 8: Uma chave Pix é formada por 9 algarismos distintos, sendo o primeiro fixado como 9. Quantas chaves distintas podem ser geradas?
a) 9 × 7!
b) 8!
c) 9!
d) 7!
e) 81 × 6!
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Resposta: b) 8!
Solução:
Como o primeiro algarismo já é fixo, restam 8 posições com 8 números distintos.
8! = 40.320 chaves possíveis
[/toggle]
Questão 9: Quantos anagramas distintos podem ser formados com a palavra “APRENDIZ”?
a) 40.300
b) 40.320
c) 40.330
d) 40.340
e) 40.350
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Resposta: b) 40.320
Solução:
A palavra tem 8 letras todas diferentes. Assim:
P(8) = 8! = 40.320 anagramas
[/toggle]
Questão 10: Quantas senhas de 10 caracteres formadas pelos símbolos {2, 2, a, A, 8, 8, 8, @, x, y} começam com 2 ou terminam com dois 8s?
a) 75.600
b) 20.160
c) 65.040
d) 60.480
e) 5.040
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Resposta: 75.600
Solução:
- Começam com 2: 9!/3! = 60.480
- Terminam com dois 8s: 8!/2!=20.160
- Ambas as condições (interseção): 7!=5.0407! = 5.040
60.480 + 20.160 − 5.040 = 75.600
[/toggle]
Questão 11: Três amigos vão dividir 8 bolas de tênis idênticas, e cada um deve receber ao menos uma. De quantas formas isso pode ser feito?
a) 15
b) 21
c) 28
d) 36
e) 45
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Três amigos vão dividir 8 bolas de tênis, e cada um deve receber ao menos uma. De quantas formas isso pode ser feito?
Resposta: 21
Solução:
Número de soluções inteiras positivas para x + y + z = 8:
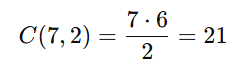
[/toggle]
Análise Combinatória: Questões Resolvidas com Explicações Passo a Passo