Questão 2. Faça um esboço do gráfico das funções quadráticas a seguir. Indique o vértice da parábola, o ponto de interseção da parábola com o eixo y e, se existirem, os zeros da função:
a) \( y = x^2 – 5x + 6 \)
b) \( y = -x^2 + 4 \)
c) \( y = x^2 – 4x + 4 \)
d) \( y = x^2 + 2x + 5 \)
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Devemos identificar para cada função quadrática: o vértice (máximo ou mínimo da parábola), o ponto de interseção com o eixo \( y \) (quando \( x = 0 \)), e os zeros da função (valores de \( x \) para os quais \( y = 0 \)).
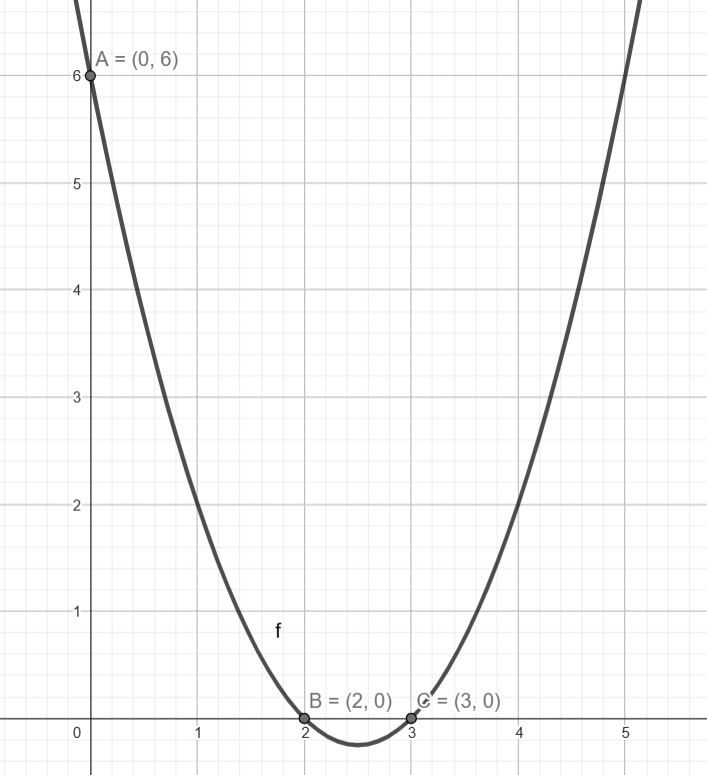
1) Analisando a função a) \( y = x^2 – 5x + 6 \)
$$ a = 1,\ b = -5,\ c = 6 $$
$$ x_v = -\frac{-5}{2 \cdot 1} = \frac{5}{2} = 2{,}5 $$
$$ y_v = (2{,}5)^2 – 5 \cdot 2{,}5 + 6 = 6{,}25 – 12{,}5 + 6 = -0{,}25 $$
Vértice: \( (2{,}5,\ -0{,}25) \)
$$ y(0) = 6 \quad \text{(interseção com o eixo } y\text{)} $$
$$ \Delta = (-5)^2 – 4 \cdot 1 \cdot 6 = 25 – 24 = 1 $$
$$ x = \frac{5 \pm \sqrt{1}}{2} = \frac{5 \pm 1}{2} $$
$$ x_1 = 3,\quad x_2 = 2 $$
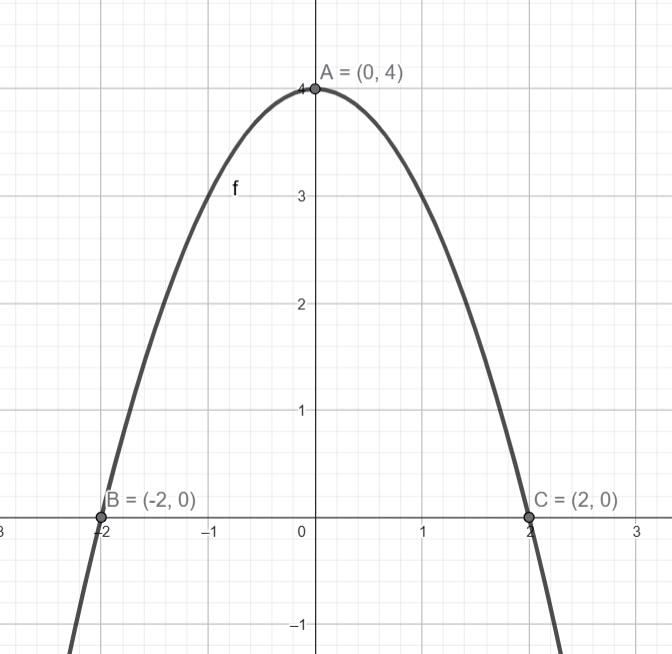
2) Analisando a função b) \( y = -x^2 + 4 \)
$$ a = -1,\ b = 0,\ c = 4 $$
$$ x_v = 0,\quad y_v = -0^2 + 4 = 4 $$
Vértice: \( (0,\ 4) \)
$$ y(0) = 4 \quad \text{(interseção com o eixo } y\text{)} $$
$$ -x^2 + 4 = 0 \Rightarrow x^2 = 4 \Rightarrow x = \pm 2 $$
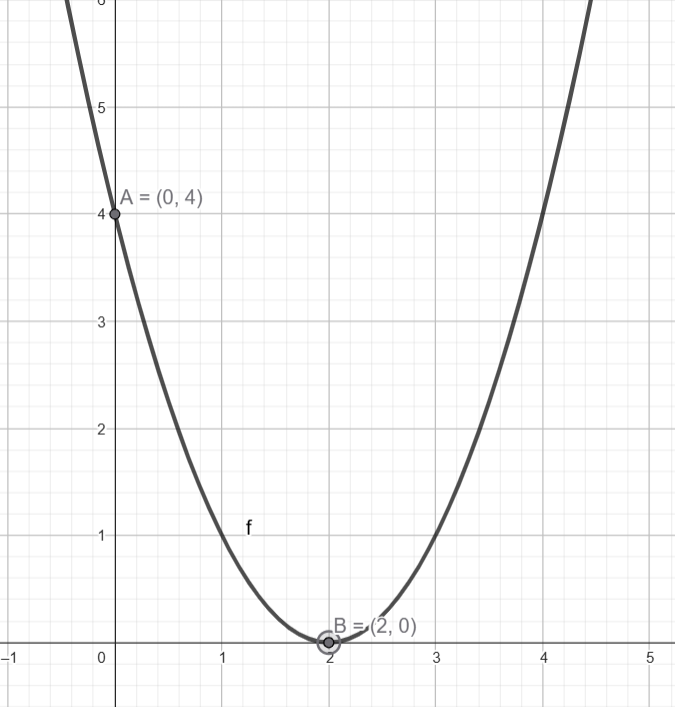
3) Analisando a função c) \( y = x^2 – 4x + 4 \)
$$ a = 1,\ b = -4,\ c = 4 $$
$$ x_v = -\frac{-4}{2 \cdot 1} = 2 $$
$$ y_v = 2^2 – 4 \cdot 2 + 4 = 4 – 8 + 4 = 0 $$
Vértice: \( (2,\ 0) \)
$$ y(0) = 4 \quad \text{(interseção com o eixo } y\text{)} $$
$$ \Delta = (-4)^2 – 4 \cdot 1 \cdot 4 = 16 – 16 = 0 $$
Raiz dupla: \( x = 2 \)
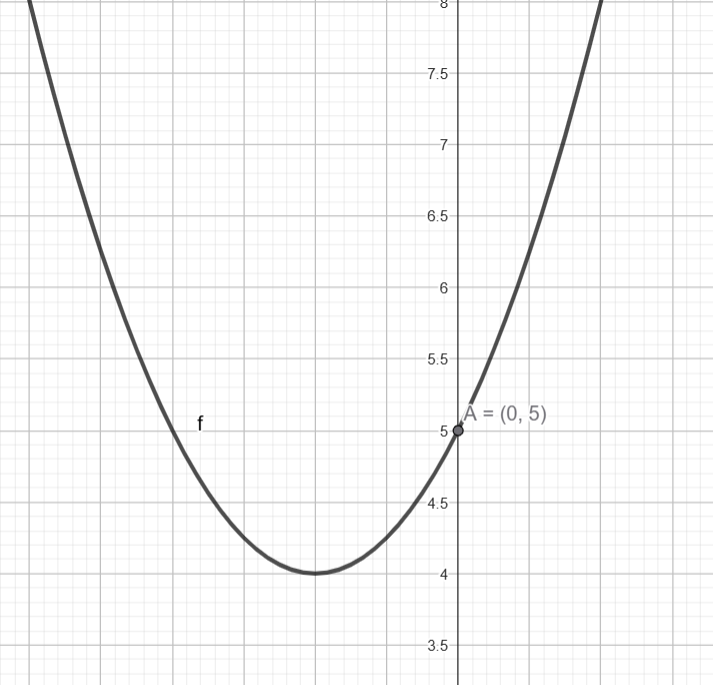
4) Analisando a função d) \( y = x^2 + 2x + 5 \)
$$ a = 1,\ b = 2,\ c = 5 $$
$$ x_v = -\frac{2}{2 \cdot 1} = -1 $$
$$ y_v = (-1)^2 + 2 \cdot (-1) + 5 = 1 – 2 + 5 = 4 $$
Vértice: \( (-1,\ 4) \)
$$ y(0) = 5 \quad \text{(interseção com o eixo } y\text{)} $$
$$ \Delta = 2^2 – 4 \cdot 1 \cdot 5 = 4 – 20 = -16 $$
Não possui raízes reais
✅ Conclusão:
- Letra a: Vértice \( (2{,}5,\ -0{,}25) \), raízes \( x = 2 \) e \( x = 3 \), interseção \( y = 6 \)
- Letra b: Vértice \( (0,\ 4) \), raízes \( x = -2 \) e \( x = 2 \), interseção \( y = 4 \)
- Letra c: Vértice \( (2,\ 0) \), raiz dupla \( x = 2 \), interseção \( y = 4 \)
- Letra d: Vértice \( (-1,\ 4) \), sem raízes reais, interseção \( y = 5 \)













