Ângulo Obtuso
Um ângulo obtuso é aquele cuja medida é maior que 90° e menor que 180°. Ele representa uma abertura mais “larga” do que um ângulo reto, mas sem se tornar raso.
Definição formal
Um ângulo \(\widehat{x}\) é obtuso se:
Ou seja: está entre 90° e 180° (exclusivos).
Propriedades principais
- O seno de um ângulo obtuso é positivo e menor que 1.
- O cosseno de um ângulo obtuso é negativo.
- Os ângulos internos de muito triângulos podem ser obtusos (um único obtuso por triângulo).
- Não pode existir mais de um ângulo obtuso em um mesmo triângulo.
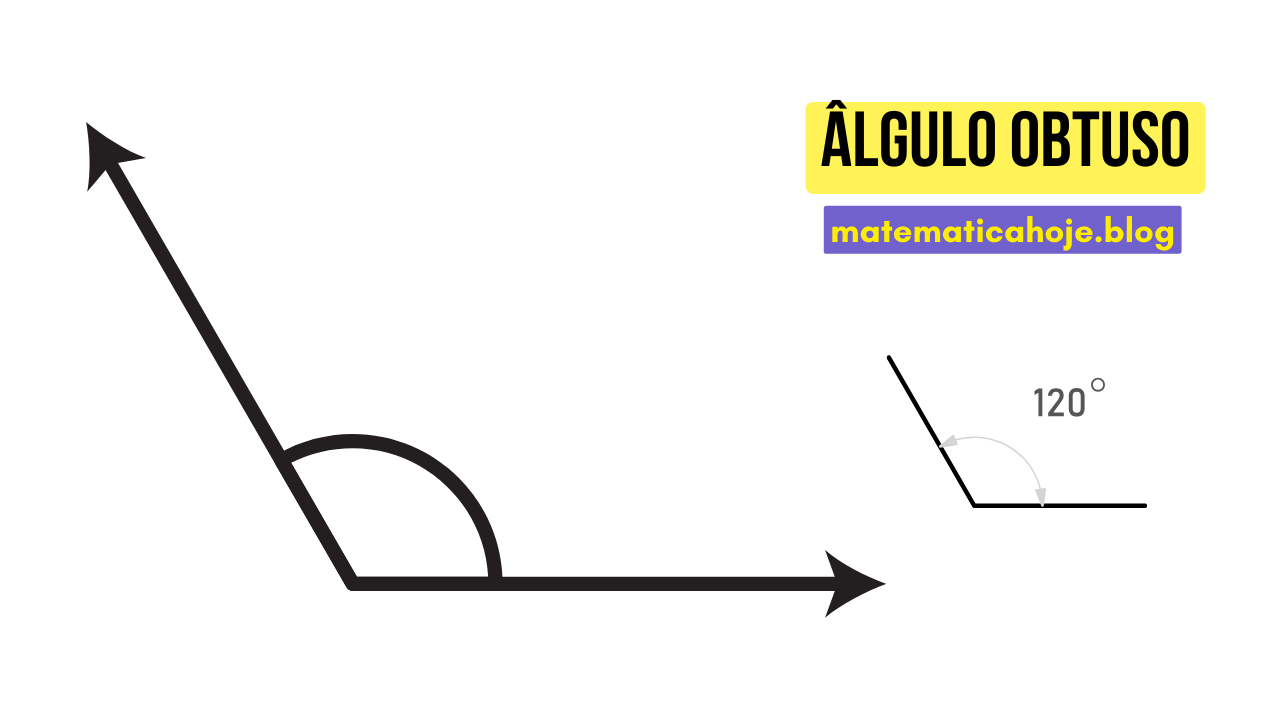
Exemplos ilustrativos
Exemplo 1: O ângulo de \(120^\circ\) é obtuso?
Sim, porque está entre 90° e 180°.
Exemplo 2: Num triângulo com ângulos 40°, 50° e \(x\), o valor de \(x\) é obtuso?
Soma dos dois primeiros: \(40 + 50 = 90\). Logo \(x = 180 – 90 = 90^\circ\). Nesse caso, é um ângulo reto, não obtuso.
📘 Exercícios de múltipla escolha — com solução
1) Qual das medidas abaixo representa um ângulo obtuso?
- \(45^\circ\)
- \(79^\circ\)
- \(135^\circ\)
- \(90^\circ\)
Ver solução
Ângulo obtuso é > 90°, < 180°. Logo 135° se enquadra.
2) Se um ângulo mede \(150^\circ\), ele é:
- Agudo
- Obtuso
- Reto
- Raso
Ver solução
Está entre 90° e 180°, logo é obtuso.
3) Num triângulo, temos dois ângulos de 55° e 30°. O terceiro ângulo é:
- \(85^\circ\)
- \(95^\circ\)
- \(100^\circ\)
- \(80^\circ\)
Ver solução
Soma dos dois dados: \(55 + 30 = 85\). O triângulo soma 180°, logo o terceiro é \(180 – 85 = 95^\circ\), obtuso.





















