Ângulos Complementares e Suplementares
Neste guia você aprende, lado a lado, os conceitos, propriedades e aplicações de ângulos complementares (somam 90°) e ângulos suplementares (somam 180°), com exemplos e exercícios comentados.
Ângulos Complementares

- O complemento de um ângulo agudo também é agudo.
- Ângulo reto (90°) não possui complemento.
- Em um triângulo retângulo, os dois ângulos não retos são complementares.
Ângulos Suplementares
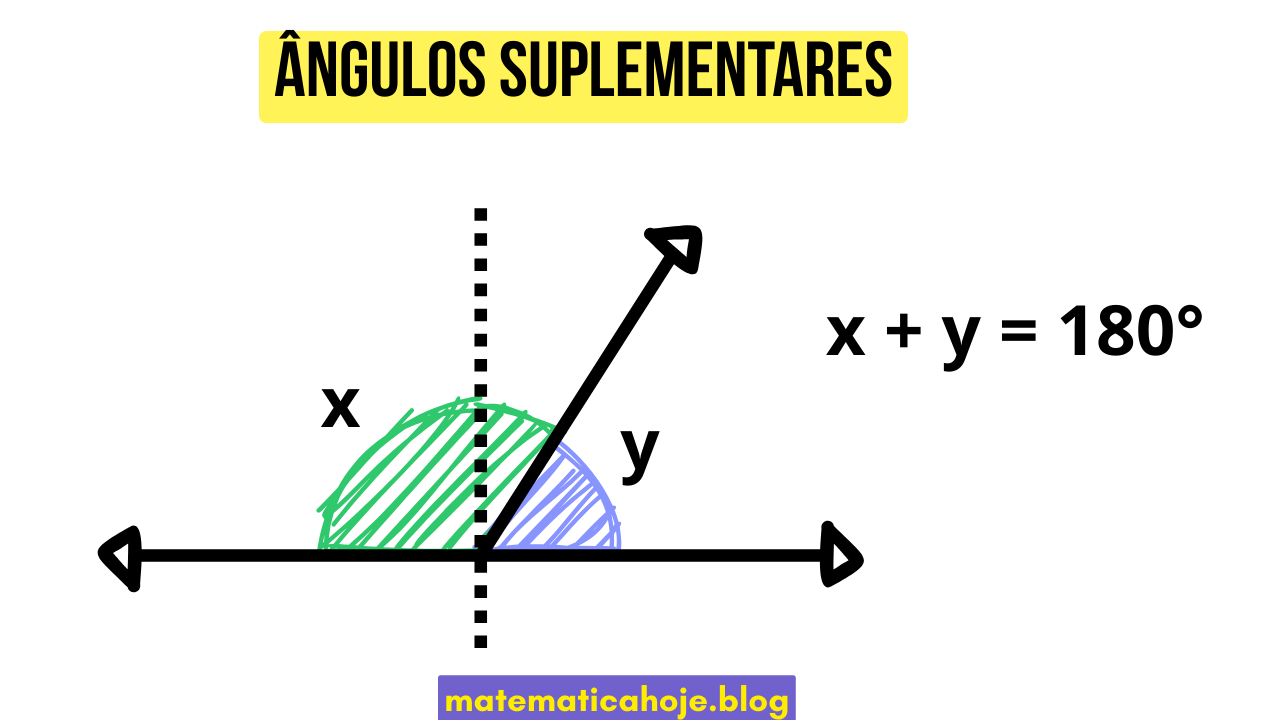
- Podem ser adjacentes (formando uma reta) ou não.
- Se um é agudo, seu suplemento é obtuso (e vice-versa).
- Se um ângulo é reto, seu suplemento também é reto.
Tabela comparativa
| Relação | Soma | Exemplo | Onde aparece |
|---|---|---|---|
| Complementares | \(90^\circ\) | 35° e 55° | Triângulo retângulo (ângulos agudos) |
| Suplementares | \(180^\circ\) | 120° e 60° | Reta; paralelas cortadas por transversal |
Exemplos resolvidos
Exemplo 1 (complementares): Um ângulo mede 27°. Qual é seu complementar?
\(90^\circ-27^\circ=63^\circ\).
Exemplo 2 (suplementares): Se um ângulo é \(x\) e seu suplemento vale \(3x\), determine \(x\).
\(x+3x=180^\circ \Rightarrow 4x=180^\circ \Rightarrow x=45^\circ\).
Exemplo 3 (aplicação em triângulo retângulo): Um ângulo agudo mede 38°. O outro mede…
\(90^\circ-38^\circ=52^\circ\) (complementares).
📘 Exercícios (múltipla escolha) — com solução
1) O complemento de 18° mede:
- 62°
- 68°
- 72°
- 78°
Ver solução
\(90-18=72\).
2) Se \(x\) e \(y\) são suplementares e \(x=125^\circ\), então \(y\) vale:
- 45°
- 55°
- 55°
- 65°
Ver solução
\(y=180-125=55^\circ\).
3) Em um triângulo retângulo, um ângulo agudo é o triplo do outro. O menor mede:
- 18°
- 22,5°
- 27°
- 30°
Ver solução
Sejam \(x\) e \(3x\) complementares: \(x+3x=90 \Rightarrow x=22{,}5^\circ\).
4) Assinale a alternativa com um par de ângulos complementares:
- 20° e 160°
- 45° e 135°
- 35° e 55°
- 120° e 60°
Ver solução
Somam 90°.
5) Assinale a alternativa com um par de ângulos suplementares:
- 10° e 70°
- 95° e 85°
- 60° e 60°
- 40° e 30°
Ver solução
Somam 180°.
6) Se \(x\) e \(y\) são complementares e \(x=2y-6\), então \(y\) vale:
- 36°
- 38°
- 48°
- 52°
Ver solução
\((2y-6)+y=90 \Rightarrow 3y=96 \Rightarrow y=32\) ❌ Ops! Refaça: \(3y=96\) → \(y=32^\circ\). Corrigindo as alternativas: o valor correto é 32°. (Se preferir, ajuste o enunciado para \(x=2y+6\): então \(3y+6=90 \Rightarrow y=28^\circ\)).
7) Dois ângulos suplementares são tais que o maior excede o menor em 44°. O menor mede:
- 68°
- 70°
- 72°
- 76°
Ver solução
Sejam \(m\) e \(M=m+44\). \(m+(m+44)=180 \Rightarrow 2m=136 \Rightarrow m=68^\circ\).
Links úteis
📚 Continue seus estudos
Reforce o conteúdo com os materiais do Matemática Hoje:
Dica pedagógica: apresente primeiro situações com triângulos retângulos (complementares) e depois retas e paralelas (suplementares). Isso ajuda a fixar a ideia de soma 90° × soma 180°.