Ângulos Notáveis: 30°, 45° e 60°
Na trigonometria, chamamos de ângulos notáveis aqueles cujos valores de seno, cosseno e tangente são frequentemente utilizados em problemas e provas: 30°, 45° e 60°. Conhecer suas razões trigonométricas é essencial para agilizar cálculos sem depender da calculadora.
Tabela dos Ângulos Notáveis
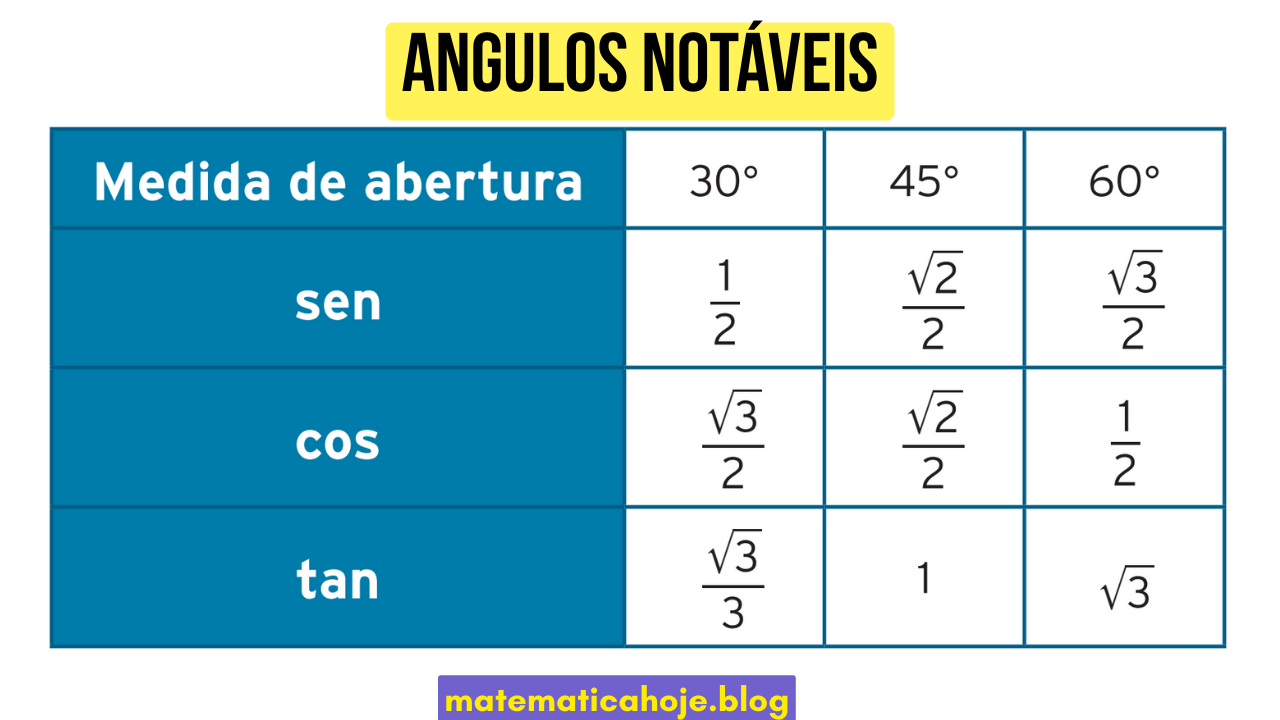
| Medida | 30° | 45° | 60° |
|---|---|---|---|
| \(\sin \theta\) | \(\tfrac{1}{2}\) | \(\tfrac{\sqrt{2}}{2}\) | \(\tfrac{\sqrt{3}}{2}\) |
| \(\cos \theta\) | \(\tfrac{\sqrt{3}}{2}\) | \(\tfrac{\sqrt{2}}{2}\) | \(\tfrac{1}{2}\) |
| \(\tan \theta\) | \(\tfrac{\sqrt{3}}{3}\) | \(1\) | \(\sqrt{3}\) |
Como deduzir os valores
- 30° e 60°: obtidos a partir do triângulo equilátero cortado pela altura, que gera um triângulo retângulo \(30°-60°-90°\).
- 45°: obtido a partir de um quadrado dividido pela diagonal, formando dois triângulos retângulos isósceles \(45°-45°-90°\).
Exemplos resolvidos
Exemplo 1: Calcule \(\sin 30^\circ\).
Da tabela: \(\sin 30^\circ = \tfrac{1}{2}\).
Exemplo 2: Determine \(\tan 60^\circ\).
Da tabela: \(\tan 60^\circ = \sqrt{3}\).
Exemplo 3: Resolva \(\cos 45^\circ\).
Da tabela: \(\cos 45^\circ = \tfrac{\sqrt{2}}{2}\).
📘 Exercícios de múltipla escolha — com gabarito
1) O valor de \(\tan 45^\circ\) é:
- \(\tfrac{\sqrt{3}}{3}\)
- 1
- \(\sqrt{3}\)
- 2
Ver solução
Da tabela, \(\tan 45^\circ = 1\).
2) O valor de \(\sin 60^\circ\) é:
- \(\tfrac{1}{2}\)
- \(\tfrac{\sqrt{2}}{2}\)
- \(\tfrac{\sqrt{3}}{2}\)
- 1
Ver solução
\(\sin 60^\circ = \tfrac{\sqrt{3}}{2}\).
3) O valor de \(\cos 30^\circ\) é:
- \(\tfrac{1}{2}\)
- \(\tfrac{\sqrt{3}}{2}\)
- \(\sqrt{3}\)
- \(\tfrac{\sqrt{2}}{2}\)
Ver solução
\(\cos 30^\circ = \tfrac{\sqrt{3}}{2}\).
4) O valor de \(\tan 30^\circ\) é:
- \(\tfrac{\sqrt{3}}{3}\)
- \(1\)
- \(\sqrt{3}\)
- \(\tfrac{1}{2}\)
Ver solução
\(\tan 30^\circ = \tfrac{\sqrt{3}}{3}\).
Links úteis
📚 Continue seus estudos
Dominar os ângulos notáveis é essencial para agilizar cálculos em trigonometria e geometria, além de ser uma habilidade muito cobrada em vestibulares e concursos.






















