Ângulos Suplementares: Definição, Exemplos e Exercícios
Na geometria, chamamos de ângulos suplementares aqueles cuja soma das medidas é igual a 180°. Eles aparecem com frequência em retas paralelas cortadas por uma transversal, polígonos e várias construções geométricas.
Definição de Ângulos Suplementares
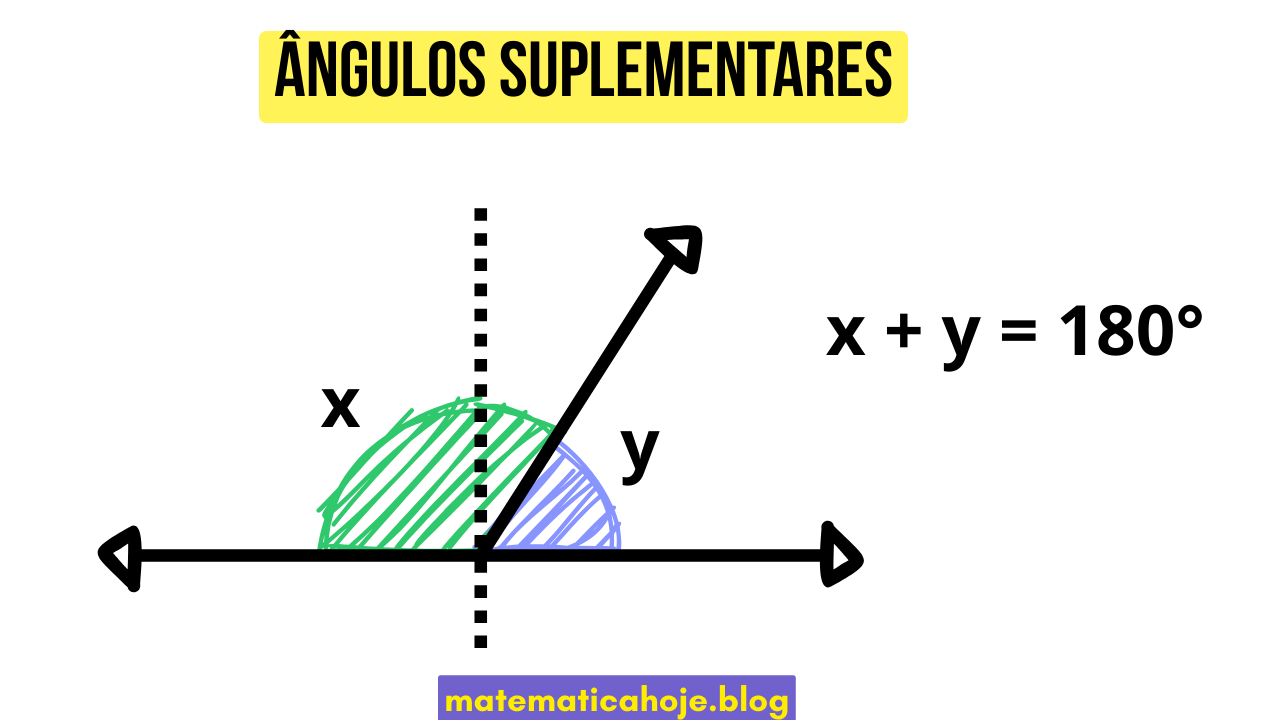
\(x + y = 180^\circ\)
- Se \(x = 120^\circ\), então o seu suplemento é \(y = 60^\circ\).
- Um ângulo raso (180°) é formado por dois ângulos suplementares adjacentes.
Propriedades Importantes
- Dois ângulos suplementares podem ser adjacentes (lado a lado) ou não.
- Se um ângulo é agudo, o seu suplemento será obtuso.
- Se um ângulo é reto (90°), o seu suplemento também será reto.
Exemplos práticos
Exemplo 1: Se um ângulo mede 75°, o seu suplemento é \(180^\circ – 75^\circ = 105^\circ\).
Exemplo 2: Em uma reta cortada por uma transversal, ângulos colaterais internos são suplementares.
📘 Exercícios de Múltipla Escolha
1) Se um ângulo mede 40°, qual é o seu suplemento?
- 120°
- 140°
- 150°
- 160°
Ver solução
180° − 40° = 140°.
2) Dois ângulos suplementares têm medidas \(x\) e \(3x\). Qual o valor de \(x\)?
- 30°
- 45°
- 60°
- 90°
Ver solução
x + 3x = 180° → 4x = 180° → x = 45°.
3) Em um quadrilátero, dois ângulos internos somam 180°. O que podemos concluir?
- São complementares
- São suplementares
- São retos
- São adjacentes
Ver solução
Quando a soma dá 180°, trata-se de ângulos suplementares.
Links Relacionados
📚 Continue seus estudos
Aprofunde-se com os materiais do Matemática Hoje:
Ângulos suplementares estão presentes em várias construções geométricas e no estudo de polígonos. São essenciais para compreender a soma dos ângulos internos.













