Arcos Congruentes
Na circunferência trigonométrica, chamamos de arcos congruentes aqueles que, mesmo possuindo medidas diferentes em graus ou radianos, determinam o mesmo ponto final na circunferência. Esse conceito é fundamental no estudo das funções trigonométricas, pois mostra que os ângulos são periódicos.
Definição
Dois arcos são congruentes quando diferem entre si por um múltiplo inteiro da volta completa da circunferência. Assim, se um arco mede \( \theta \), outro arco será congruente a ele se tiver medida:
\(\theta + k \cdot 360^\circ \quad \text{ou} \quad \theta + k \cdot 2\pi \ \text{rad}, \quad k \in \mathbb{Z}\)
Exemplo Visual
Observe os arcos abaixo. Embora as medidas sejam diferentes (\(\frac{\pi}{3}\), \(\frac{7\pi}{3}\), \(\frac{13\pi}{3}\)), todos terminam no mesmo ponto da circunferência, logo são congruentes.
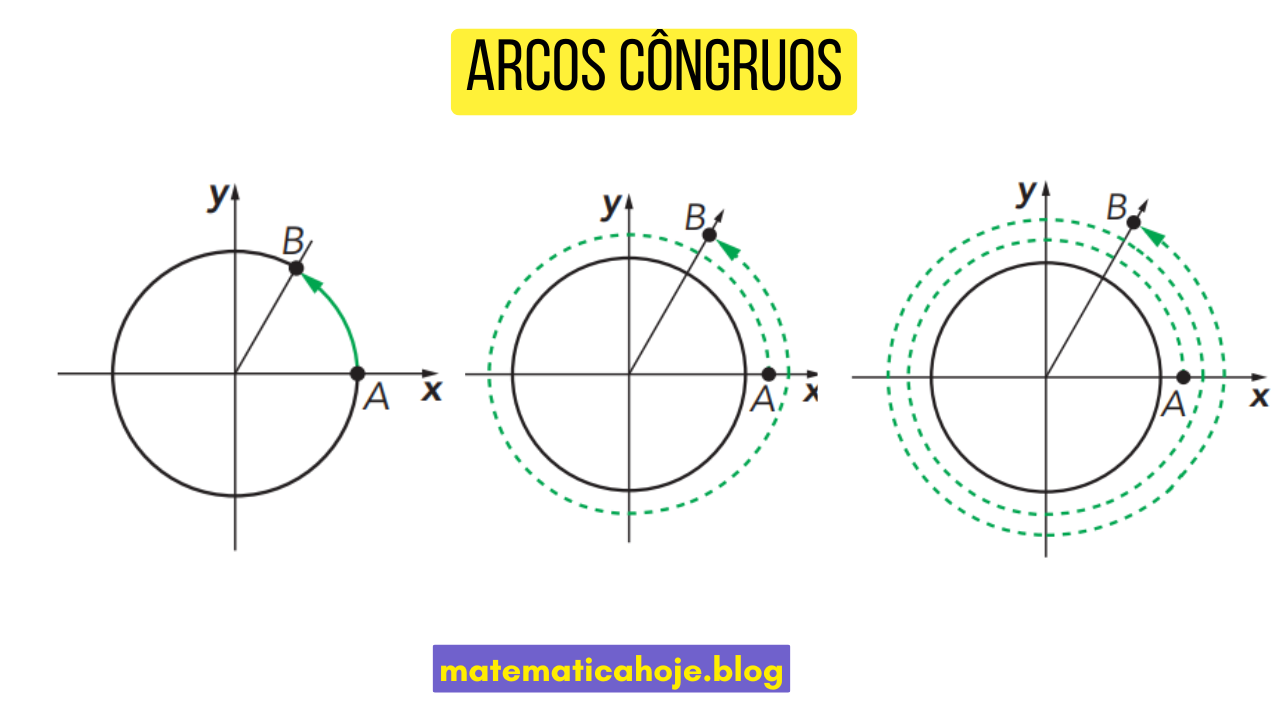
O texto abaixo ilustra bem essa ideia:
Exemplo Resolvido
Exemplo:
Mostre que os arcos de \(60^\circ\), \(420^\circ\) e \(780^\circ\) são congruentes.
Solução:
- \(60^\circ\) é o arco inicial.
- \(420^\circ = 60^\circ + 360^\circ\), logo é congruente a \(60^\circ\).
- \(780^\circ = 60^\circ + 2\cdot 360^\circ\), logo também é congruente a \(60^\circ\).
Portanto, todos determinam o mesmo ponto na circunferência.
📘 Exercícios de múltipla escolha
1) Qual dos ângulos abaixo é congruente a \(45^\circ\)?
- \(60^\circ\)
- \(90^\circ\)
- \(405^\circ\)
- \(120^\circ\)
Ver solução
\(405^\circ = 45^\circ + 360^\circ\), logo é congruente a \(45^\circ\).
2) Quais ângulos são congruentes a \(\frac{\pi}{6}\)?
- \(\frac{7\pi}{6}\)
- \(\frac{13\pi}{6}\)
- \(-\frac{11\pi}{6}\)
- \(\pi\)
Ver solução
\(\frac{13\pi}{6} = \frac{\pi}{6} + 2\pi\) e \(-\frac{11\pi}{6} = \frac{\pi}{6} – 2\pi\). Logo, ambos são congruentes a \(\frac{\pi}{6}\).
3) O ângulo \(750^\circ\) é congruente a qual dos seguintes?
- \(30^\circ\)
- \(60^\circ\)
- \(30^\circ\)
- \(120^\circ\)
Ver solução
\(750^\circ = 2\cdot 360^\circ + 30^\circ\). Logo, é congruente a \(30^\circ\).
4) O arco \(-\frac{5\pi}{4}\) é congruente a:
- \(-\frac{\pi}{4}\)
- \(\frac{3\pi}{4}\)
- \(\pi\)
- \(\frac{\pi}{6}\)
Ver solução
\(-\frac{5\pi}{4} + 2\pi = \frac{3\pi}{4}\). Portanto, é congruente a \(\frac{3\pi}{4}\).
5) Qual dos ângulos abaixo é congruente a \(150^\circ\)?
- \(510^\circ\)
- \(200^\circ\)
- \(100^\circ\)
- \(-30^\circ\)
Ver solução
\(510^\circ = 150^\circ + 360^\circ\). Portanto, é congruente a \(150^\circ\).
6) Qual dos ângulos é congruente a \(-60^\circ\)?
- \(30^\circ\)
- \(150^\circ\)
- \(300^\circ\)
- \(120^\circ\)
Ver solução
\(-60^\circ + 360^\circ = 300^\circ\). Logo, \(-60^\circ\) é congruente a \(300^\circ\).
7) O ângulo \(\frac{25\pi}{6}\) é congruente a qual valor?
- \(\frac{\pi}{6}\)
- \(\frac{5\pi}{6}\)
- \(\frac{\pi}{6}\)
- \(\pi\)
Ver solução
\(\frac{25\pi}{6} – 4\pi = \frac{\pi}{6}\). Portanto, o arco é congruente a \(\frac{\pi}{6}\).
📚 Continue estudando
Os arcos congruentes mostram a ideia de periodicidade da trigonometria, essencial para compreender funções como seno, cosseno e tangente.






















