Área da Esfera
A esfera é um dos principais corpos redondos. Todos os pontos da sua superfície estão à mesma distância do centro; essa distância é o raio \(r\). Para revisar conceitos, propriedades e o volume, veja: Esfera e Exercício Esfera. Compare também com sólidos como Cubo e Paralelepípedo.
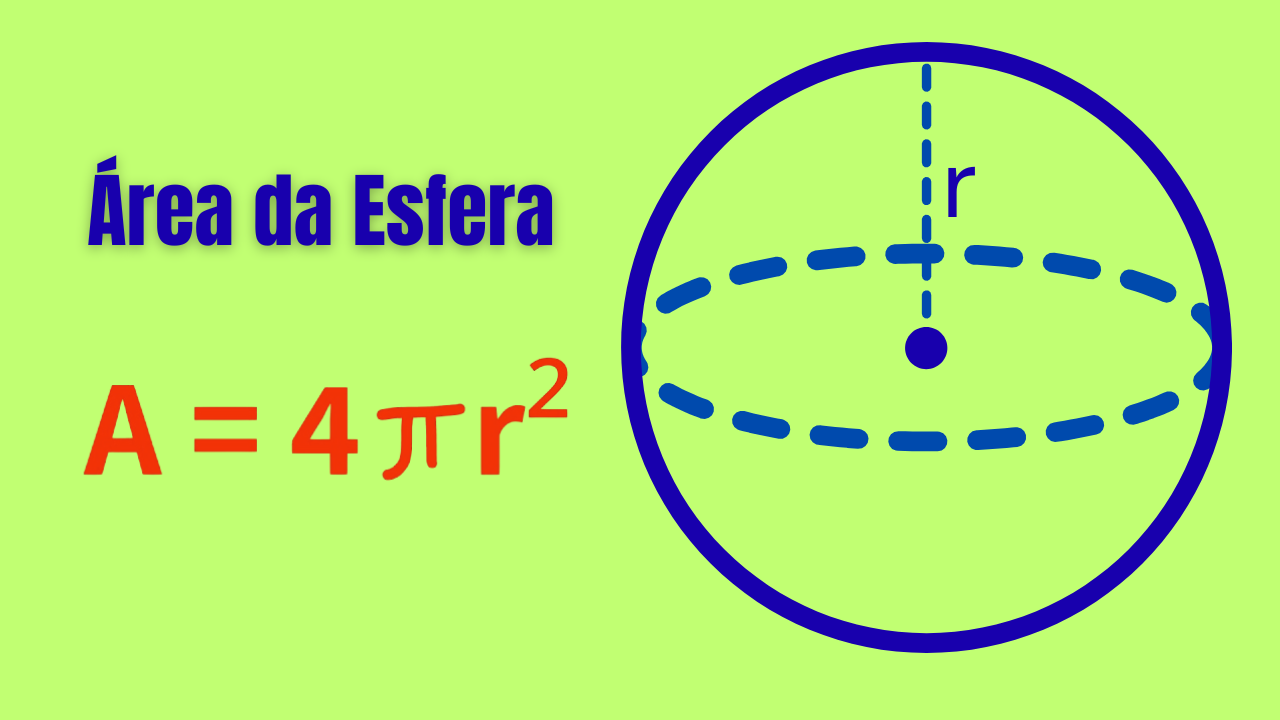
Fórmula principal
- \(A\): área da superfície (unidades quadradas, como cm² ou m²);
- \(\pi \approx 3{,}14159\);
- \(r\): raio da esfera.
Variações úteis
- Em função do diâmetro \(d=2r\): \(A=\pi d^{2}\)
- Isolando o raio a partir da área: \( \displaystyle r=\sqrt{\frac{A}{4\pi}} \)
- Escala: se o raio é multiplicado por \(k\), a área multiplica por \(k^{2}\) (crescimento quadrático).
Relação com o volume
Para a esfera, a derivada do volume em relação ao raio é igual à área da superfície: \( \displaystyle \frac{d}{dr}\!\left(\frac{4}{3}\pi r^{3}\right) = 4\pi r^{2}=A \). Essa identidade conecta exercícios de volume e de área.
Erros comuns
- Usar \(r^{3}\) (volume) em vez de \(r^{2}\) (área).
- Confundir diâmetro com raio (lembre: \(r=\dfrac{d}{2}\)).
- Responder em unidades cúbicas por engano—área é sempre em unidades quadradas.
Exemplos resolvidos
Exemplo 1. Calcule a área de uma esfera de raio \(r=7\text{ cm}\).
Ver solução
Exemplo 2. Uma esfera tem área \(A=144\pi\ \text{cm}^{2}\). Qual é o raio?
Ver solução
Exemplo 3. Uma esfera está inscrita em um cubo de aresta \(12\ \text{cm}\). Determine a área da esfera.
Ver solução
Exercícios (múltipla escolha)
1) Calcule a área de uma esfera de raio \(4\ \text{cm}\).
- \(32\pi\ \text{cm}^{2}\)
- \(48\pi\ \text{cm}^{2}\)
- \(64\pi\ \text{cm}^{2}\)
- \(96\pi\ \text{cm}^{2}\)
Ver solução
Resposta: C.
2) Uma esfera tem diâmetro \(20\ \text{cm}\). Qual é sua área?
- \(200\pi\ \text{cm}^{2}\)
- \(300\pi\ \text{cm}^{2}\)
- \(350\pi\ \text{cm}^{2}\)
- \(400\pi\ \text{cm}^{2}\)
Ver solução
Resposta: D.
3) Se \(A=324\pi\ \text{cm}^{2}\), então o raio vale:
- \(7\ \text{cm}\)
- \(8\ \text{cm}\)
- \(9\ \text{cm}\)
- \(10\ \text{cm}\)
Ver solução
Resposta: C.
4) Uma esfera metálica tem raio \(0{,}75\ \text{m}\). Qual é a área aproximada em m²?
- \(4{,}50\ \text{m}^{2}\)
- \(7{,}07\ \text{m}^{2}\)
- \(9{,}42\ \text{m}^{2}\)
- \(12{,}57\ \text{m}^{2}\)
Ver solução
Resposta: B.
5) O raio de uma esfera aumentou \(15\%\). O aumento percentual da área é, aproximadamente:
- \(15\%\)
- \(30\%\)
- \(32{,}25\%\)
- \(45\%\)
Ver solução
Resposta: C.
Materiais relacionados
Continue estudando com nossos conteúdos internos:
- Esfera — definição, elementos e propriedades.
- Exercício Esfera — listas com respostas e passo a passo.
- Corpos redondos — visão geral com comparações.
- Cubo e Paralelepípedo — para contrastar fórmulas e unidades.






















