Área Polígono regular

Área de Polígonos Regulares — fórmulas, exemplos e exercícios

Área de Polígonos Regulares

Um polígono regular tem todos os lados e todos os ângulos internos congruentes. Nesta página, você aprende as fórmulas mais úteis para calcular a área — por apótema e perímetro, pelo lado, pelo raio circunscrito — e vê exemplos práticos passo a passo.

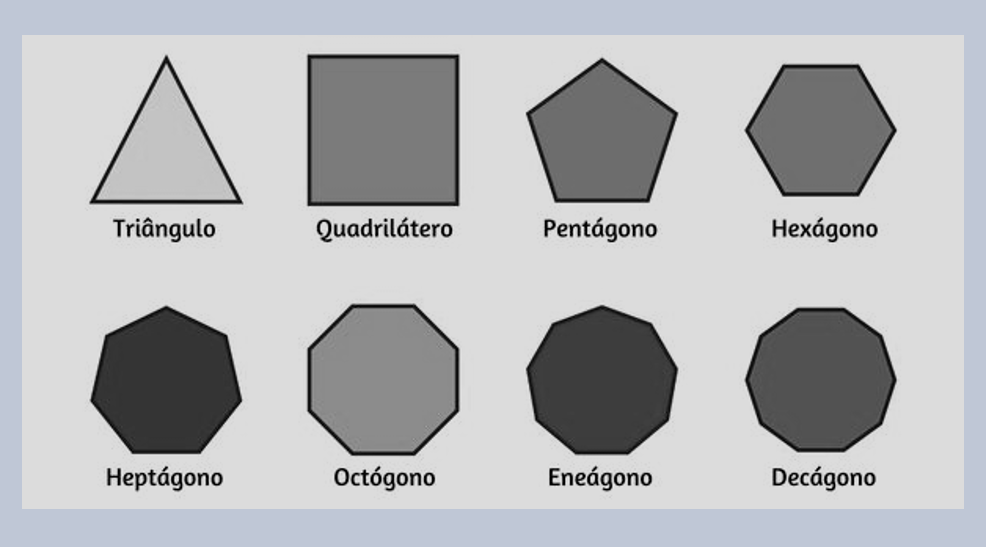
Formas regulares: triângulo, quadrado, pentágono, hexágono, heptágono, octógono, eneágono e decágono
Alguns polígonos regulares: triângulo, quadrado, pentágono, … decágono.
Reforce conteúdos base: Área do Triângulo, Lei dos Senos, Lei dos Cossenos, Área do Trapézio e Triângulos: tipos e propriedades.

Conceitos essenciais

  • n: número de lados; s: comprimento do lado; P: perímetro (\(P=n\,s\)).
  • apótema \(a\): distância do centro a um lado (raio da circunferência inscrita).
  • raio circunscrito \(R\): distância do centro a um vértice.
  • Ângulo central: \(\dfrac{360^\circ}{n}\). Cada setor central gera um triângulo isósceles.

Fórmulas da área (todas empilhadas)

\[ \textbf{1) Por apótema e perímetro:}\quad \boxed{A=\frac{P\cdot a}{2}} \]
\[ \text{com } P=n\,s \Rightarrow A=\frac{n\,s\,a}{2} \]
\[ \textbf{2) Pelo lado}\ (s):\quad \boxed{A=\frac{n\,s^{2}}{4\,\tan\!\left(\frac{\pi}{n}\right)}} \]
\[ \text{e } a=\frac{s}{2\,\tan\!\left(\frac{\pi}{n}\right)} \]
\[ \textbf{3) Pelo raio circunscrito}\ (R):\quad \boxed{A=\frac{1}{2}\,n\,R^{2}\,\sin\!\left(\frac{2\pi}{n}\right)} \]
\[ \text{e } s=2R\sin\!\left(\frac{\pi}{n}\right),\quad a=R\cos\!\left(\frac{\pi}{n}\right) \]

As fórmulas acima são equivalentes. Escolha a que usa os dados fornecidos no problema. Em provas, é comum fornecer o lado \(s\) (use a #2) ou o apótema \(a\) (use a #1).

Exemplos resolvidos (situação-problema)

1

Hexágono regular — apótema e perímetro

O piso de um quiosque será um hexágono regular. O apótema medido é \(a=3\,\text{m}\) e cada lado mede \(s=3{,}5\,\text{m}\).

Dados
\(n=6\), \(a=3\,\text{m}\), \(s=3{,}5\,\text{m}\).

Pergunta: qual é a área total do piso?

Ver solução
\[ \begin{aligned} P&=n\,s=6\cdot 3{,}5=21\\ A&=\frac{P\,a}{2}=\frac{21\cdot 3}{2}= \boxed{31{,}5\ \text{m}^2} \end{aligned} \]
2

Octógono regular — pelo lado

Uma moldura tem formato de octógono regular de lado \(s=12\,\text{cm}\).

Dados
\(n=8\), \(s=12\,\text{cm}\).

Pergunta: qual é a área interna da moldura?

Ver solução
\[ \begin{aligned} A&=\frac{n\,s^2}{4\,\tan\!\left(\frac{\pi}{n}\right)}\\ &=\frac{8\cdot 12^2}{4\,\tan(\pi/8)}\\ &=\frac{8\cdot 144}{4\,\tan(22{,}5^\circ)}\\ &=\frac{1152}{4\cdot 0{,}41421356\ldots}\\ &\approx \boxed{695{,}9\ \text{cm}^2} \end{aligned} \]
3

Pentágono regular — pelo raio R

Um brasão tem forma de pentágono regular inscrito numa circunferência de raio \(R=20\,\text{cm}\).

Dados
\(n=5\), \(R=20\,\text{cm}\).

Pergunta: qual é a área do brasão?

Ver solução
\[ \begin{aligned} A&=\tfrac12\,n\,R^2\,\sin\!\left(\tfrac{2\pi}{n}\right)\\ &=\tfrac12\cdot 5\cdot 20^2\cdot \sin(72^\circ)\\ &=1000\cdot 0{,}951056516\ldots\\ &\approx \boxed{951{,}06\ \text{cm}^2} \end{aligned} \]
4

Quadrado — conferindo com base × altura

Um canteiro é um quadrado regular de lado \(s=4\,\text{m}\).

Dados
\(n=4\), \(s=4\,\text{m}\).

Pergunta: calcule a área pelas duas abordagens.

Ver solução
\[ \begin{aligned} \text{Fórmula do lado: }A&=\frac{n s^2}{4\tan(\pi/n)}=\frac{4\cdot 16}{4\tan 45^\circ}=\frac{64}{4\cdot 1}=16\\ \text{Paralelogramo: }A&=s^2=4^2=16\\ &\Rightarrow \boxed{16\ \text{m}^2} \end{aligned} \]

Erros comuns (e como evitar)

  • Confundir apótema com raio circunscrito. No regular vale \(a=R\cos\!\left(\frac{\pi}{n}\right)\), mas são grandezas diferentes.
  • Usar graus em calculadora configurada para radianos (ou vice-versa). Verifique o modo antes de usar \(\tan\), \(\sin\) e \(\cos\).
  • Perímetro errado. Lembre: \(P=n\,s\). No hexágono, por exemplo, \(P=6s\).

Exercícios propostos (múltipla escolha)

1

Apótema e lado

Um decágono regular tem lado \(s=10\,\text{cm}\) e apótema \(a=15{,}4\,\text{cm}\).

A área é:

  • A) \(500\ \text{cm}^2\)
  • B) \(600\ \text{cm}^2\)
  • C) \(770\ \text{cm}^2\)
  • D) \(1\,540\ \text{cm}^2\)
Gabarito
\[ \begin{aligned} P&=n s=10\cdot 10=100\\ A&=\tfrac{P a}{2}=\tfrac{100\cdot 15{,}4}{2}=\boxed{770\ \text{cm}^2}\ (\text{C}) \end{aligned} \]
2

Pelo lado (triângulo equilátero)

Um triângulo equilátero tem lado \(s=9\,\text{cm}\).

A área é:

  • A) \(27\sqrt{3}\ \text{cm}^2\)
  • B) \(\dfrac{81\sqrt{3}}{4}\ \text{cm}^2\)
  • C) \(40{,}5\ \text{cm}^2\)
  • D) \(81\ \text{cm}^2\)
Gabarito
\[ A=\frac{n s^2}{4\tan(\pi/n)}\ (n{=}3)=\frac{3\cdot 9^2}{4\tan 60^\circ} =\frac{243}{4\sqrt{3}}=\boxed{\frac{81\sqrt{3}}{4}}\ (\text{B}) \]
3

Hexágono pelo raio

Num mosaico, cada peça é um hexágono regular inscrito em circunferência de raio \(R=8\,\text{cm}\).

A área de uma peça é:

  • A) \(96\ \text{cm}^2\)
  • B) \(128\ \text{cm}^2\)
  • C) \(166{,}3\ \text{cm}^2\)
  • D) \(192\ \text{cm}^2\)
Gabarito
\[ \begin{aligned} A&=\tfrac12\,n\,R^2\,\sin\left(\tfrac{2\pi}{n}\right),\ n=6\\ &=\tfrac12\cdot 6\cdot 8^2\cdot \sin 60^\circ\\ &=3\cdot 64\cdot \tfrac{\sqrt3}{2} =96\sqrt3\approx \boxed{166{,}3\ \text{cm}^2}\ (\text{C}) \end{aligned} \]

Materiais do Matemática Hoje

Relacionadas

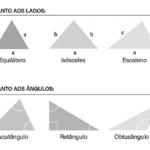
Triângulos — tipos e propriedades

Ângulos Excêntricos na Circunferência

Área do triângulo equilátero

"Artigo escrito por"

Picture of Adriano Rocha

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.

Nos ajude compartilhando esse post 😉

Facebook
WhatsApp
Twitter
Pinterest

👉🟢+ de 90 Mapas Mentais de Matemática

Veja também...

Questões

Conteúdo

Banca

Instagram Facebook Youtube