Área de uma Coroa Circular
Aprenda a calcular a área da região entre dois círculos concêntricos. Fórmula, exemplos e exercícios resolvidos.
1) O que é uma coroa circular?
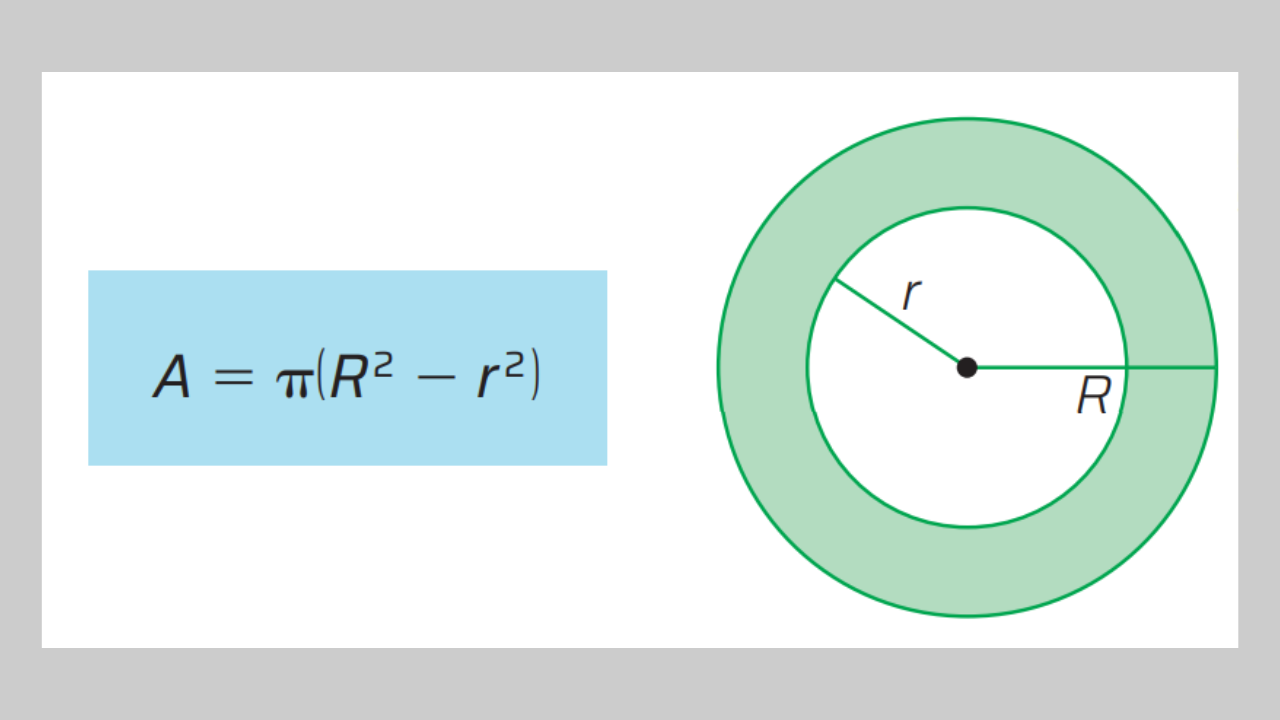
Uma coroa circular é a região do plano delimitada por dois círculos concêntricos (com o mesmo centro), um de raio maior \(R\) e outro de raio menor \(r\). Essa figura aparece em problemas de geometria, arquitetura, engenharia e até no cálculo de áreas de terrenos circulares.
2) Fórmula da área da coroa circular
A área da coroa é a diferença entre a área do círculo maior e a área do círculo menor:
Onde:
\(R\) = raio do círculo maior
\(r\) = raio do círculo menor (\(R > r\))
3) Exemplo resolvido
Exemplo: Uma coroa circular tem raio maior \(R=10\) cm e raio menor \(r=6\) cm. Calcule a área.
Mostrar solução passo a passo
Aplicando a fórmula:
\(A=\pi (R^2 – r^2)=\pi(10^2 – 6^2)=\pi(100-36)=\pi\cdot64=64\pi\; \text{cm}^2\)
Aproximando: \(A\approx201,06\;\text{cm}^2\) (\(\pi\approx3,14\)).
4) Observações importantes
- Se \(r=0\), a coroa circular vira um círculo comum (\(A=\pi R^2\)).
- Se \(R=r\), a área da coroa é zero (não existe região entre os círculos).
- Unidades de área sempre ao quadrado: cm², m², km² etc.
5) Exercícios práticos
1. Calcule a área de uma coroa circular de \(R=7\) cm e \(r=4\) cm.
Ver solução
\(A=\pi(7^2-4^2)=\pi(49-16)=33\pi\; \text{cm}^2\).
2. Um jardim é delimitado por dois círculos concêntricos, com \(R=12\) m e \(r=9\) m. Qual é a área da faixa circular?
Ver solução
\(A=\pi(12^2-9^2)=\pi(144-81)=63\pi\;\text{m}^2\approx197,92\;\text{m}^2\).






















