Área do Circulo

Área do Círculo — fórmulas, exemplos e exercícios

Área do Círculo

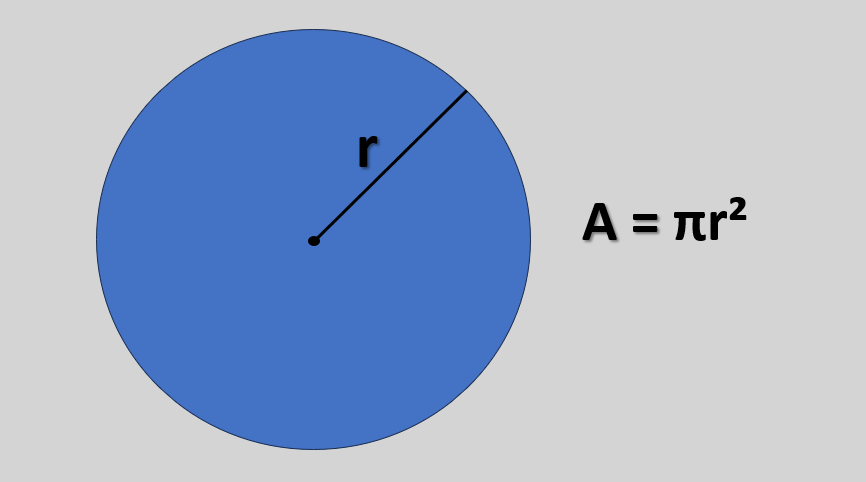
A área do círculo mede a “região pintada” do disco. A fórmula mais usada é \( \mathbf{A=\pi r^2} \), onde \(r\) é o raio. A seguir você vê variações úteis (em função do diâmetro e do comprimento da circunferência), além de exemplos práticos, setor circular e exercícios.

Círculo com raio r e a fórmula A = π r²
Disco de raio \(r\). A área é \(A=\pi r^2\).
Reforce a base em: Área do Triângulo (decomposição), Polígonos Regulares (aproximação do círculo por polígonos), Lei dos Senos e Lei dos Cossenos (geometria do setor).

Fórmulas da área (todas empilhadas)

\[ \textbf{1) Fórmula básica:}\quad \boxed{A=\pi r^2} \]
\[ \textbf{2) Em função do diâmetro}\ (d=2r):\quad \boxed{A=\pi\left(\frac{d}{2}\right)^2=\frac{\pi d^2}{4}} \]
\[ \textbf{3) Em função do comprimento da circunferência}\ (C=2\pi r):\quad \boxed{A=\frac{C^2}{4\pi}} \]
\[ \textbf{4) Setor circular de ângulo central }\theta:\quad \boxed{A_{\text{setor}}=\frac{\theta}{360^\circ}\,\pi r^2} \quad \text{ou}\quad \boxed{A_{\text{setor}}=\frac{\theta}{2}\,r^2\ \ (\theta\text{ em rad})} \]
\[ \textbf{5) Coroa circular (anel):}\quad \boxed{A=\pi\left(R^2-r^2\right)} \]

Exemplos resolvidos (situação-problema)

1

Raio conhecido

Uma tampa circular de pote tem raio \(r=7\,\text{cm}\).

Dados
\(r=7\,\text{cm}\).

Qual é a área da tampa?

Ver solução
\[ \begin{aligned} A&=\pi r^2\\ &=\pi\cdot 7^2\\ &=49\pi\\ &\approx \boxed{153{,}94\ \text{cm}^2} \end{aligned} \]
2

Diâmetro informado

Um jardim circular tem diâmetro \(d=20\,\text{m}\).

Dados
\(d=20\,\text{m}\Rightarrow r=10\,\text{m}\).

Qual é a área do jardim?

Ver solução
\[ \begin{aligned} A&=\frac{\pi d^2}{4}\\ &=\frac{\pi\cdot 20^2}{4}\\ &=\frac{400\pi}{4}\\ &=100\pi\\ &\approx \boxed{314{,}16\ \text{m}^2} \end{aligned} \]
3

A partir do comprimento C

A borda de uma mesa circular tem comprimento \(C=31{,}4\,\text{cm}\).

Dados
\(C=31{,}4\,\text{cm}\).

Qual é a área do tampo?

Ver solução
\[ \begin{aligned} A&=\frac{C^2}{4\pi}\\ &=\frac{31{,}4^2}{4\pi}\\ &=\frac{985{,}96}{12{,}56637\ldots}\\ &\approx \boxed{78{,}5\ \text{cm}^2} \end{aligned} \]

Dica: esta é a mesma área de um disco com \(r\approx 5\,\text{cm}\) (pois \(C\approx 2\pi r\)).

4

Setor circular

Um identificador de pizza marca uma fatia como setor de raio \(r=12\,\text{cm}\) e ângulo central \(\theta=60^\circ\).

Dados
\(r=12\,\text{cm}\), \(\theta=60^\circ\).

Qual é a área dessa fatia?

Ver solução
\[ \begin{aligned} A_{\text{setor}}&=\frac{\theta}{360^\circ}\,\pi r^2\\ &=\frac{60^\circ}{360^\circ}\cdot \pi\cdot 12^2\\ &=\frac{1}{6}\cdot \pi\cdot 144\\ &=24\pi\\ &\approx \boxed{75{,}40\ \text{cm}^2} \end{aligned} \]

Para mais prática com ângulos e triângulos, veja Lei dos Senos e Lei dos Cossenos.

Erros comuns (e como evitar)

  • Confundir raio com diâmetro. Lembre: \(d=2r\). Se o enunciado der o diâmetro, use \(A=\dfrac{\pi d^2}{4}\).
  • Trocar \(\pi\) por um valor aproximado errado. Use \(\pi\approx 3{,}1416\) (ou deixe em termos de \(\pi\)).
  • Setor em radianos. Se \(\theta\) vier em rad, use \(A_{\text{setor}}=\dfrac{\theta}{2}r^2\). Em graus, \(A_{\text{setor}}=\dfrac{\theta}{360^\circ}\pi r^2\).

Para decompor regiões circulares em figuras simples, consulte também área do triângulo, área do trapézio e área do paralelogramo.

Exercícios propostos (múltipla escolha)

1

Raio simples

Uma moeda tem raio \(r=4\,\text{m}\) (modelo ampliado).

A área é:

  • A) \(12\pi\ \text{m}^2\)
  • B) \( \mathbf{16\pi\ \text{m}^2\ (\approx 50{,}27\ \text{m}^2)} \)
  • C) \(32\pi\ \text{m}^2\)
  • D) \(8\pi\ \text{m}^2\)
Gabarito
\[ A=\pi r^2=\pi\cdot 4^2=16\pi\approx \boxed{50{,}27\ \text{m}^2}\ (\text{B}) \]
2

Com diâmetro

Um relógio circular tem diâmetro \(d=14\,\text{cm}\).

A área do mostrador é:

  • A) \(36\pi\ \text{cm}^2\)
  • B) \(49\pi\ \text{cm}^2\)
  • C) \( \mathbf{153{,}94\ \text{cm}^2} \)
  • D) \(196\pi\ \text{cm}^2\)
Gabarito
\[ A=\frac{\pi d^2}{4}=\frac{\pi\cdot 14^2}{4}=\frac{196\pi}{4}=49\pi\approx \boxed{153{,}94\ \text{cm}^2}\ (\text{C}) \]
3

A partir de C

Um canteiro circular possui comprimento de borda \(C=62{,}8\,\text{m}\).

A área do canteiro é:

  • A) \( \mathbf{313{,}9\ \text{m}^2} \)
  • B) \(628\ \text{m}^2\)
  • C) \(157{,}0\ \text{m}^2\)
  • D) \(100\pi\ \text{m}^2\)
Gabarito
\[ \begin{aligned} A&=\frac{C^2}{4\pi}=\frac{62{,}8^2}{4\pi}\\ &=\frac{3943{,}84}{12{,}56637\ldots}\\ &\approx \boxed{313{,}9\ \text{m}^2}\ (\text{A}) \end{aligned} \]
4

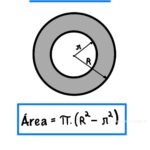
Coroa circular (anel)

Um anel metálico tem raio externo \(R=10\,\text{cm}\) e interno \(r=6\,\text{cm}\).

A área do anel é:

  • A) \(64\ \text{cm}^2\)
  • B) \( \mathbf{201{,}06\ \text{cm}^2} \)
  • C) \(64\pi\ \text{cm}^2\)
  • D) \( \mathbf{64\pi\ \text{cm}^2\ (\approx 201{,}06\ \text{cm}^2)} \)
Gabarito
\[ A=\pi(R^2-r^2)=\pi(100-36)=\pi\cdot 64=64\pi\approx \boxed{201{,}06\ \text{cm}^2}\ (\text{D}) \]

Quer mais prática? Veja o nosso banco de questões e os mapas mentais de geometria.

Materiais do Matemática Hoje

Relacionadas

Triângulo Acutângulo

Lei dos Senos

Igualdade entre pares de ângulos opostos no Triângulo

"Artigo escrito por"

Picture of Adriano Rocha

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.

Nos ajude compartilhando esse post 😉

Facebook
WhatsApp
Twitter
Pinterest

👉🟢+ de 90 Mapas Mentais de Matemática

Veja também...

Questões

Conteúdo

Banca

Instagram Facebook Youtube