Área do Losango: fórmula com diagonais, exemplos resolvidos e exercícios
Tudo o que você precisa para calcular a superfície do losango e dominar questões do ENEM e de concursos.
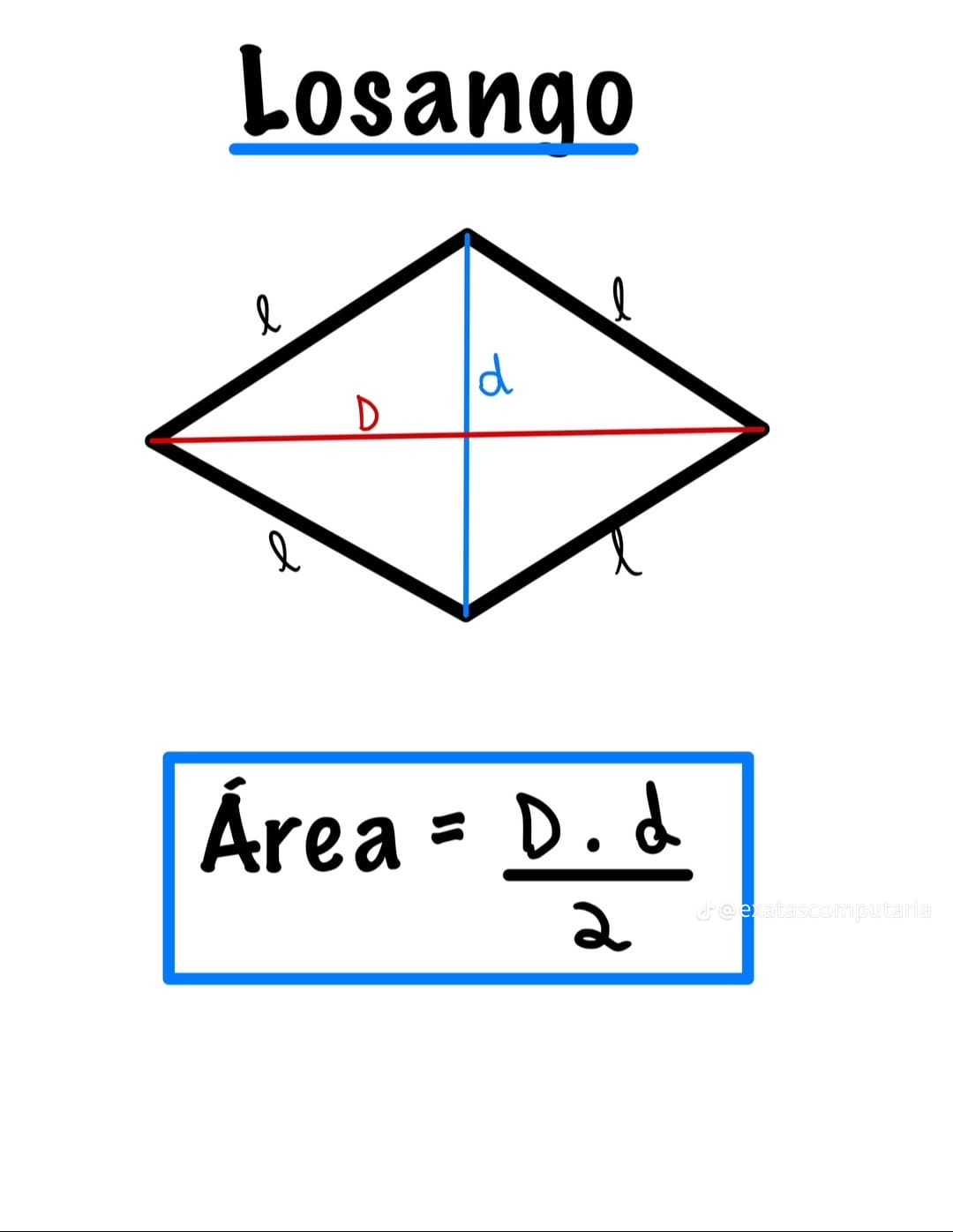
Definição e propriedades
O losango é um quadrilátero com quatro lados congruentes. É um tipo de paralelogramo, portanto possui lados opostos paralelos e ângulos opostos iguais. Suas diagonais são perpendiculares e bissetam os ângulos, dividindo-se ao meio.
Fórmula principal da área
\[ A = \frac{D\cdot d}{2} \]
Basta multiplicar as diagonais e dividir por 2. A unidade resultante é ao quadrado (cm², m², …).
Relações úteis
\[ l = \sqrt{\left(\frac{D}{2}\right)^2+\left(\frac{d}{2}\right)^2} \]
\[ A = l^2\cdot \sin(\theta) \]
Onde \(l\) é o lado do losango e \(\theta\) é um ângulo interno.
Aproveite também: Mapas Mentais de Matemática • ENEM Matemática • Banco de Questões
📘 Fórmulas sem dor de cabeça
Baixe o eBook Fórmulas Matemática e tenha todas as expressões de Geometria Plana na ponta dos dedos.
Exemplos resolvidos
Exemplo 1 Básico
No losango, \(D=10\,\text{cm}\) e \(d=6\,\text{cm}\). Encontre a área.
Ver solução
\[ A=\frac{D\cdot d}{2}=\frac{10\cdot 6}{2}=\frac{60}{2}=30\,\text{cm}^2. \]
Exemplo 2 Intermediário
A área de um losango é \(60\,\text{cm}^2\) e a diagonal maior mede \(D=12\,\text{cm}\). Determine a diagonal menor.
Ver solução
\[ 60=\frac{12\cdot d}{2}\Rightarrow 60=6d\Rightarrow d=10\,\text{cm}. \]
Exemplo 3 Aplicado
Num losango de lado \(l=5\,\text{cm}\) e ângulo interno \(\theta=60^\circ\), calcule a área.
Ver solução
\[ A=l^2\sin\theta=5^2\cdot \sin60^\circ=25\cdot \frac{\sqrt3}{2}=12{,}5\sqrt3\approx 21{,}65\,\text{cm}^2. \]
Exercícios de múltipla escolha (com gabarito)
Resolva antes de abrir as respostas. Questões de dificuldade progressiva.
1) Em um losango, \(D=12\,\text{cm}\) e \(d=8\,\text{cm}\). A área é:
Gabarito e solução
\(A=\dfrac{12\cdot 8}{2}=48\Rightarrow\) Letra C.
2) A área de um losango vale \(A=84\,\text{cm}^2\). Se \(D=14\,\text{cm}\), então \(d\) é:
Gabarito e solução
\(84=\dfrac{14\cdot d}{2}\Rightarrow 84=7d\Rightarrow d=12\,\text{cm}\Rightarrow\) Letra C.
3) Um terreno em forma de losango tem diagonais \(D=24\,\text{m}\) e \(d=10\,\text{m}\). Quantos sacos de sementes são necessários se cada saco cobre \(8\,\text{m}^2\)?
Gabarito e solução
Área: \(A=\dfrac{24\cdot 10}{2}=120\). Sacos: \(120/8=15\Rightarrow\) Letra C.
4) Num losango, \(D=12\) e \(d=5\). O perímetro é:
Gabarito e solução
Lado: \(l=\sqrt{(6)^2+(2{,}5)^2}=\sqrt{36+6{,}25}=\sqrt{42{,}25}=6{,}5\).
Perímetro: \(4l=26\Rightarrow\) Letra B.
5) Em um losango, dobrar ambas as diagonais faz a área:
Gabarito e solução
\(A\propto D\cdot d\). Se \(D\to 2D\) e \(d\to 2d\), então \(A\to 4A\Rightarrow\) Letra B.
6) Um losango tem lado \(l=10\) (perímetro \(P=40\)) e diagonal maior \(D=16\). A diagonal menor é:
Gabarito e solução
\(l^2=(D/2)^2+(d/2)^2\Rightarrow 100=8^2+(d/2)^2\Rightarrow (d/2)^2=36\Rightarrow d=12\Rightarrow\) Letra C.
7) Para um losango de lado fixo \(l\), a área máxima ocorre quando o ângulo interno é:
Gabarito e solução
\(A=l^2\sin\theta\). O máximo de \(\sin\theta\) é 1, em \(\theta=90^\circ\Rightarrow\) Letra C (quadrado).
8) Se \(A=200\,\text{cm}^2\) e \(d=20\,\text{cm}\), então a diagonal maior \(D\) vale:
Gabarito e solução
\(200=\dfrac{D\cdot 20}{2}\Rightarrow 200=10D\Rightarrow D=20\,\text{cm}\Rightarrow\) Letra C.
Dicas finais
- Confirme sempre qual é a diagonal maior (\(D\)) e a menor (\(d\)) — embora a fórmula funcione para a multiplicação em qualquer ordem.
- Em problemas com lado e ângulo, use \(A=l^2\sin(\theta)\).
- Para perímetro, lembre-se de que \(l=\sqrt{(D/2)^2+(d/2)^2}\) e \(P=4l\).













